ホーム
数学
特色２　数学的な見方、考え方を体得するために

特色
2

数学的な見方、
考え方を
体得するために

学びをひろげる場面や問題を解決する場面で役に立つ考え方を， $たいせつな考え方$ として顕在化させ，わかりやすく表現しました。大切な考え方を働かせている場面には，本文中に下線をひき，その右側にどんな考え方を使っているかを示す「標識」を配置しています。
ここで示したことは，数学の学習を進める上で大切にしてほしい数学的な見方・考え方であるとともに，数学の学習だけではなく，他教科の学習や生活の中でも役に立つ「生きる力」につながります。

授業の中で働かせた数学的な見方・考え方を顕在化させ，わかりやすく表現しました。

$イメージ画像:3年p72$ $イメージ画像:1年p65$

標識の種類

使用場面を「問題発見」「問題解決」の２つに分け，区別して示しました。
これらの標識をくり返し目にすることで，数学的な見方・考え方を自然に体得できます。

新しい問題を見つけるなどして
学びをひろげるときに
役に立つ考え方

$きまりを見つける$ $範囲をひろげる$

$条件をかえる$ $逆向きに考える$

問題発見の場面で…

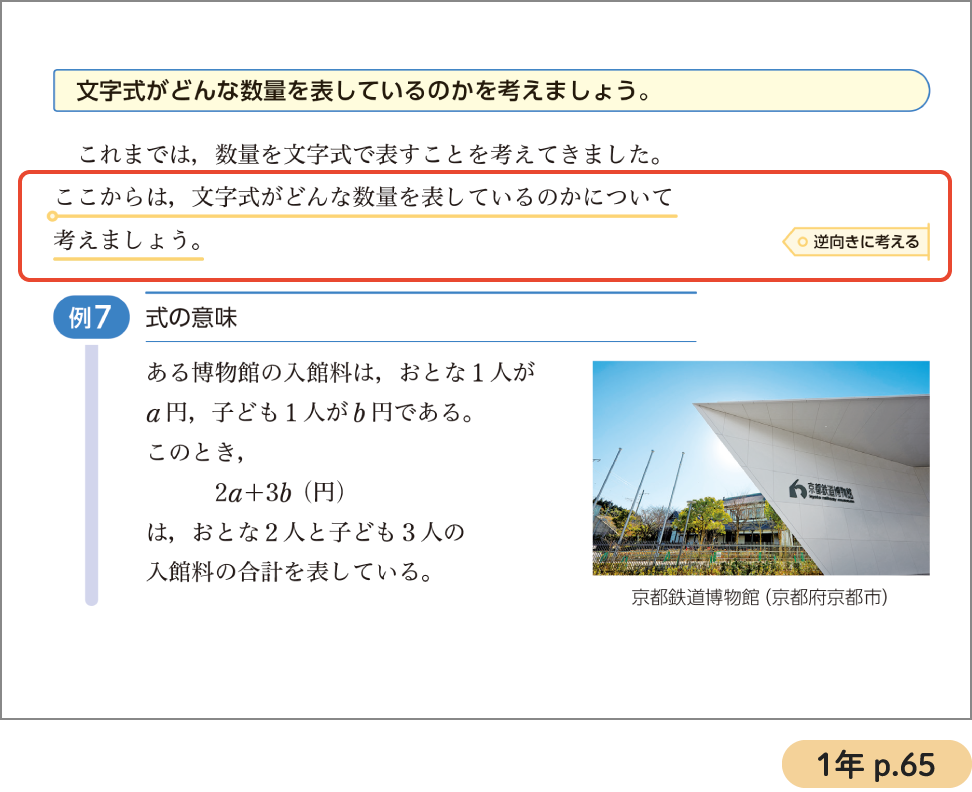
$イメージ画像:1年p65$

「数量を文字式で表す」ことを学習したあとに，逆向きに考えて，「文字式がどんな数量を表しているのかを考える」という学習につなげていきます。
このように，今まで考えたことと逆向きに考えて，新たな学習につなげていく場面に，「逆向きに考える」という標識を置いています。

問題を解決するときに
役に立つ考え方

$同じように考える$ $すでに学んだ形にする$

$結論からさかのぼる$ $分類整理する$

問題解決の場面で…

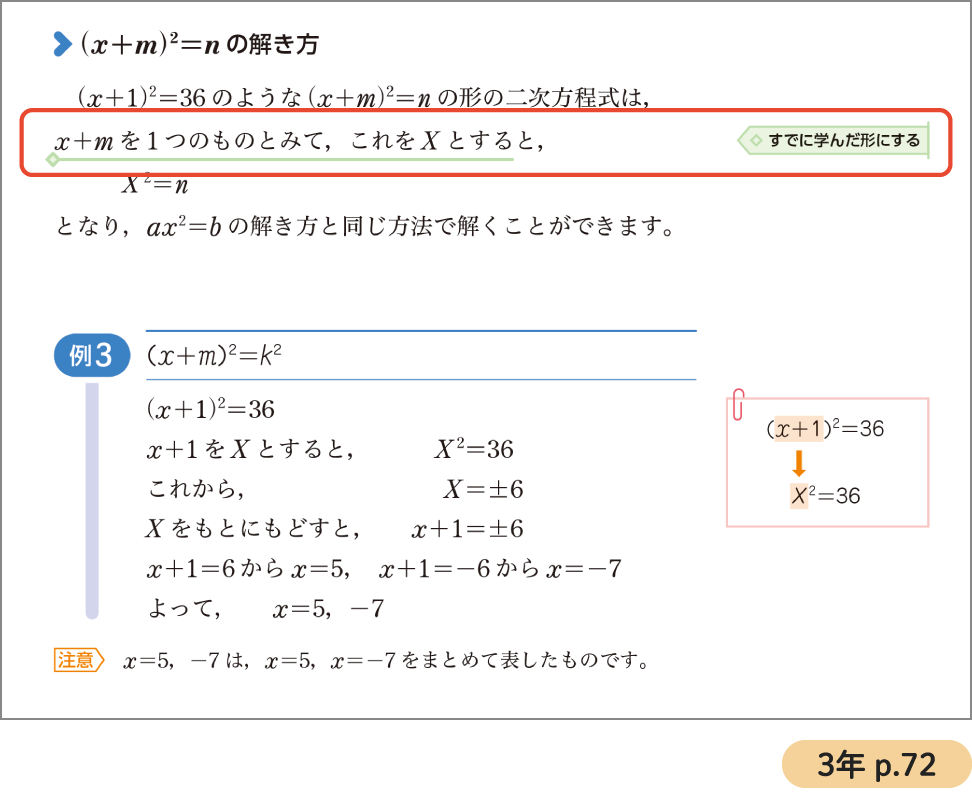
$イメージ画像:3年p72$

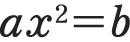$(x+m)2=n$ のような形の二次方程式を学習していく場面で，ある部分を１つのものとみて，すでに学んだ $ax2=b$ の形にして考えていきます。
このように，過去に学んだ形にして考えればこれから取り組む新しい問題も解決できるのではないかと考えられる場面に，「すでに学んだ形にする」という標識を置いています。

巻頭では，「たいせつな考え方」がどのようなところに置かれているかを，生徒にもわかりやすいように丁寧に説明しています。

$啓林館が大切にしていること$

啓林館では，「数学的な見方・考え方を体得できるようにすること」を以前から大切にしています。
数学的な見方・考え方をわかりやすく示すため，紙面での表現の仕方に工夫を重ねています。
今回は，「問題発見」と「問題解決」の数学的な見方・考え方を区別して明示するという工夫をしています。

$イメージ画像:啓林館が大切にしていること$

編集委員からのメッセージ

学習指導要領では，「数学を活用して問題解決する方法を理解するとともに，自ら問題を見いだし，解決するための構想を立て，実践し，その過程や結果を評価・改善する」など，生徒の主体的な取り組みの質的充実が期待されています。それゆえ，何をどう捉え，どう考えるかを具体的な状況に即して整理，自覚し，実践することが大切です。うまくいったことはもちろん，途中までではあったとしても考え続けたこと，結果は間違いであったとしても解決に向けて考えたことを，考え方に焦点を当てて価値付けたいですね。