

本校は令和元年度からSSH(スーパーサイエンスハイスクール)の指定校になっており,数学の分野でも様々な活動が行われている。今回,主に夏休みを利用してSSH数学講座「黄金比」と題して講義を行った。 前編では,その教材の前半部分を紹介し,主に黄金比と自然界のつながりについて述べている。後編では教材の後半部分(15)~(26) を紹介し,黄金比を数学的に分析している。それに併せ,実際に講座を受けた生徒の感想や講座の意義についても述べる。
| 講 座 名: | SSH数学公開講座「黄金比」 |
| 日 時: | 令和2年8月21日(金)及び25日(火) |
| 時 間: | 毎回約2時間(計4時間)(興味がある一部の生徒にはさらに2時間) |
| 対 象: | 1,2年生 16名+理科教員2名 |
| 配布資料: | A4で約60ページ |
| 内 容: | 黄金比 |
前 編
(1)ユークリッドの問題から
(2)ペンタグラマの中に現れる黄金比
(3)黄金比と正五角形の作図
(4)もうひとつの比-白銀比-
(5)黄金長方形-正方形がいくつとれるか-
(6)フィボナッチ数列と黄金比
(7)フィボナッチ数列とパスカルの三角形
(8)対数螺旋と黄金比
(9)連分数
(10)黄金比の連分数展開
(11)連分数による有理数近似
(12)黄金比は最も有理数を寄せ付けない
(13)植物の葉の並びと黄金比
(14)ひまわりと松ぼっくりにでてくる螺旋
後 編
(15)黄金比にさらなる数学的メスを入れる
(16)フィボナッチからの分数列が最も黄金比に近いことの証明
(17)T 値で黄金比に近づく数列を分類する
(18)フィボナッチからの分数列が黄金比に近づく速さ
(19)黄金比の周りの有理数分布
(20)白銀比に数学的メスを入れる
(21)白銀比とペル数
(22)ペル数による分数列が白銀比に近づく速さ
(23)青銅比に数学的メスを入れる
(24)分数列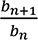 が青銅比に近づく速さ
が青銅比に近づく速さ
(25)貴金属比の中の黄金比
(26)神様が造った黄金比が自然を操る
さて,前編の(6)でも論じたように,フィボナッチの数列は,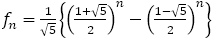 で表され,
で表され, は
は より大きくなったり,小さくなったりを繰り返しながら,
より大きくなったり,小さくなったりを繰り返しながら,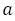 に近づいていく。
に近づいていく。
黄金比 は無理数で,
は無理数で,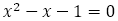 の正の解である。したがって,整数
の正の解である。したがって,整数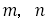 に対して
に対して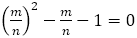 になることはない。換言すれば,
になることはない。換言すれば,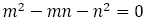 になることはない。
になることはない。
しかし, が
が の“よい”近似値であれば
の“よい”近似値であれば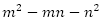 の値は0ではないが値は整数でたとえれば±1等,その絶対値は小さい数でなければならない。
の値は0ではないが値は整数でたとえれば±1等,その絶対値は小さい数でなければならない。
フィボナッチ数列から導かれる分数 について,この計算をすると
について,この計算をすると

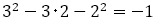
 のように,その値は±1である。
のように,その値は±1である。
いま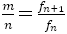 のとき,
のとき, であることを示そう。
であることを示そう。
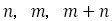 はこの順にフィボナッチ数列の途中の項とする。 隣接する
はこの順にフィボナッチ数列の途中の項とする。 隣接する に対して
に対して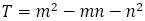 の値を考える。
の値を考える。
次の隣接する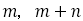 に対して
に対して の値は,
の値は,
つまり隣接する項では,絶対値は同じで,マイナスをかけたものである。実際,フィボナッチの数列で最初から計算すると,

よって,フィボナッチの数列では が成り立つ。
が成り立つ。
よって,フィボナッチ数列から導かれる分数は の“よい”近似値である。
の“よい”近似値である。
一方, なので,
なので,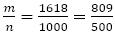 として
として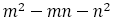 の値を計算すると,
の値を計算すると, となり,分母が500と大きい割には“よい”近似値とはいえない。
となり,分母が500と大きい割には“よい”近似値とはいえない。
ところで,前述したユークリッドが黄金比について言及した図形の問題で,一辺が の正方形と,縦が
の正方形と,縦が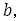 横が
横が の長方形の面積が等しくなる場合,
の長方形の面積が等しくなる場合,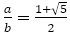 であることを述べたが,同じ図形で一辺が
であることを述べたが,同じ図形で一辺が の正方形と縦が
の正方形と縦が 横が
横が である長方形を考えると,
である長方形を考えると, であるので,2 つの面積は等しくはならないが,差が1 になる。
であるので,2 つの面積は等しくはならないが,差が1 になる。
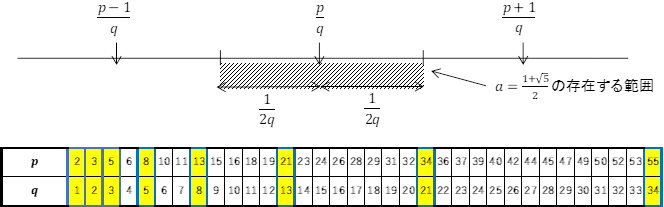
図は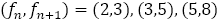 の場合を示したものであるが,確かに面積の差は1である。ユークリッドはこのような背景から,あの問題をつくったのかもしれない。
の場合を示したものであるが,確かに面積の差は1である。ユークリッドはこのような背景から,あの問題をつくったのかもしれない。
また,以上の議論の副産物として, は既約分数であることがわかる。なぜなら,もし
は既約分数であることがわかる。なぜなら,もし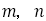 の公約数を
の公約数を とすれば,
とすれば,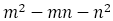 も約数として
も約数として をもつことになる。しかし
をもつことになる。しかし であるから,
であるから,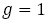 である。
である。
よって,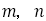 は互いに素である。
は互いに素である。
さて今度は隣り合うフィボナッチからの分数の差について考えてみよう。
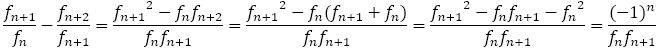
よって,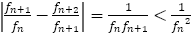
さらに,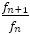 は
は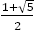 に交互に大きくなったり小さくなったりして近づいていくから,
に交互に大きくなったり小さくなったりして近づいていくから,
よって, が成立する。
が成立する。
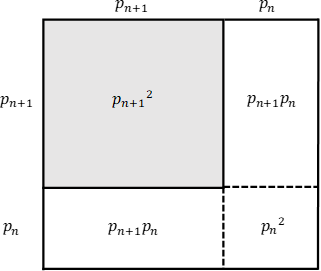
以下の表は分母 を1,2,3,4…と動かし,
を1,2,3,4…と動かし, と
と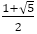 の差が最も小さくなるように分子
の差が最も小さくなるように分子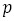 を定めている。明らかに数列
を定めている。明らかに数列 は
は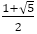 に近づく。しかし,その近づき方は緩慢である。なぜならば,
に近づく。しかし,その近づき方は緩慢である。なぜならば, が近似値になるためには,図の網掛けの中に
が近似値になるためには,図の網掛けの中に があればよい。よって,
があればよい。よって,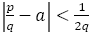 である。
である。
しかし,フィボナッチからの分数の場合には,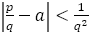 が成り立つので,分母が小さい割に,はるかによい近似値となることがわかる。
が成り立つので,分母が小さい割に,はるかによい近似値となることがわかる。
さてもう一度,前述したフィボナッチ数列からできる隣接する分数の差について再び考えてみる。
前述の式: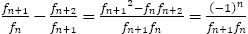 から分母はそれぞれの分数の分母の積,分子の絶対値は1 である。
から分母はそれぞれの分数の分母の積,分子の絶対値は1 である。
次のような問題を考えてみよう。
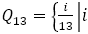 は自然数
は自然数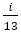 は既約分数
は既約分数
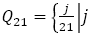 は自然数
は自然数 は既約分数
は既約分数
において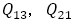 の距離を求めよ。
の距離を求めよ。
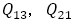 の距離とは
の距離とは に対して,
に対して,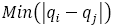 を意味する。
を意味する。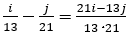 であるので,
であるので,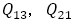 の距離になるには,
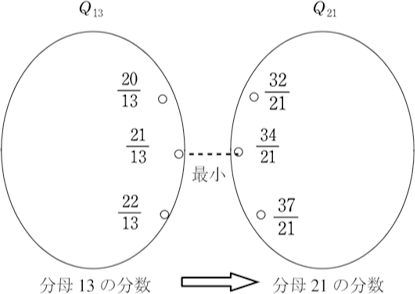
の距離になるには, の絶対値が最小にならなければならない。21と13は互いに素であるので,
の絶対値が最小にならなければならない。21と13は互いに素であるので,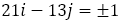 は必ず解を持つ。これは不定方程式の問題である。
は必ず解を持つ。これは不定方程式の問題である。
実際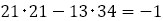 となり,
となり,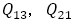 の距離は
の距離は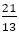 と
と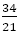 の距離に等しく,その距離は
の距離に等しく,その距離は である。
である。
こうした観点からみると,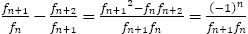 の絶対値はフィボナッチの分数において,分母が
の絶対値はフィボナッチの分数において,分母が から
から に変わるとき
に変わるとき どうしの距離になるようになっている。換言すれば,分母が変わるとき,一番近い相手になるよう分子が変化していることがわかる。
どうしの距離になるようになっている。換言すれば,分母が変わるとき,一番近い相手になるよう分子が変化していることがわかる。
ところで,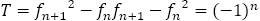 の両辺を
の両辺を で割ると,
で割ると, ・・・①
・・・①
一方, は
は ・・・②を満たす。
・・・②を満たす。
上式で①から②を引くと,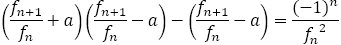
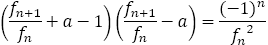
 ただし,
ただし,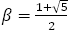
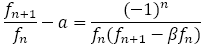
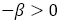 に気をつけると
に気をつけると は
は
 より大きくなったり小さくなったりを繰り返しながら,
より大きくなったり小さくなったりを繰り返しながら, に近づくことは前にも述べたが,
に近づくことは前にも述べたが,
さらに,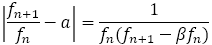
 より,
より, と
と の距離より次の分数
の距離より次の分数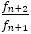 と
と との距離の方が必ず小さくなることがわかる。
との距離の方が必ず小さくなることがわかる。
ところで,フィボナッチの数列 で
で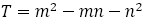 の値を考えた。
の値を考えた。
次の隣接する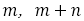 に対して
に対して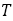 の値は,
の値は,
であったので,フィボナッチの数列でなくても,フィボナッチ型の数列,つまり を満たす数列ならば,
を満たす数列ならば,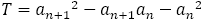 の絶対値は一定で,プラスマイナスを繰り返す。つまり,
の絶対値は一定で,プラスマイナスを繰り返す。つまり,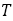 は初項と第2 項によって決まり,
は初項と第2 項によって決まり,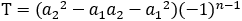 である。よって,
である。よって,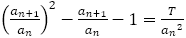 が成り立ち
が成り立ち
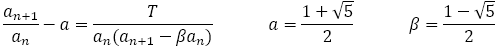
が成立する。
したがって,フィボナッチ型の数列も,プラスマイナスを繰り返しながら に近づいていくことがわかる。しかも
に近づいていくことがわかる。しかも が増加すれば確実に
が増加すれば確実に との距離は縮まる。
との距離は縮まる。
次の表は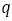 において分母を1 から34 まで連続的に変化させ,それぞれに対して
において分母を1 から34 まで連続的に変化させ,それぞれに対して が一番黄金比
が一番黄金比 に近くなるように分子
に近くなるように分子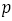 を選んでいる。そして
を選んでいる。そして に対して
に対して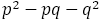 の値を計算している。表からわかるように,この値が±1 になるのはフィボナッチの数列のところだけである。それ以外のところは±1になっていない。なぜだろうか。
ちなみにフィボナッチの数列のところが±1になるのは,前に示している。
それ以外のところが±1にならない理由を考えたい。
の値を計算している。表からわかるように,この値が±1 になるのはフィボナッチの数列のところだけである。それ以外のところは±1になっていない。なぜだろうか。
ちなみにフィボナッチの数列のところが±1になるのは,前に示している。
それ以外のところが±1にならない理由を考えたい。
そのことを示すために に対してこれから示す一連の操作を行う。
に対してこれから示す一連の操作を行う。

― 操作 ―
フィボナッチの数列から導かれる分数の数列で の次に現れるのは
の次に現れるのは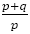 である。
である。
逆に の前の分数は
の前の分数は である。
である。
そこで,分数 に対して
に対して を対応させる関数
を対応させる関数 を考える。
を考える。
いわば,フィボナッチの分数列を1つ前に“逆流”させる関数である。
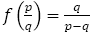 (既約でない場合は予め約分する)
(既約でない場合は予め約分する)
前掲の分数 に対して関数
に対して関数 を含んだ以下のようなアルゴリズムを考える。
を含んだ以下のようなアルゴリズムを考える。
まず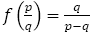 を計算し,その値が
を計算し,その値が かどうかを判断する。
かどうかを判断する。
もしそうならば に対して
に対して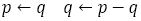 ,つまり
,つまり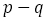 を新しい分母に,
を新しい分母に,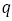 を新しい分子にして
を新しい分子にして を施す。つまり
を施す。つまり
 を計算する。そして再度
を計算する。そして再度 かどうかの判断を行うループを行っていく。
かどうかの判断を行うループを行っていく。
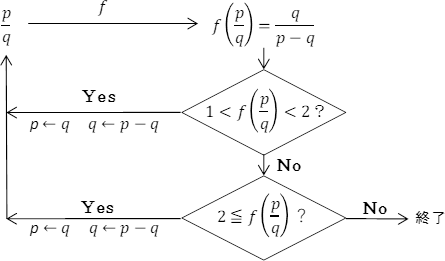
もし, でないならば,次の判断
でないならば,次の判断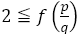 かどうかの判断に進む。もしそうなら再び
かどうかの判断に進む。もしそうなら再び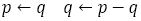 を施し,
を施し, を施すループに戻っていく。もし,
を施すループに戻っていく。もし, でもないし
でもないし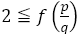 でもなければそこで終了する。
でもなければそこで終了する。
具体的に,上掲の表にある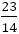 でこの操作をしてみよう。
でこの操作をしてみよう。
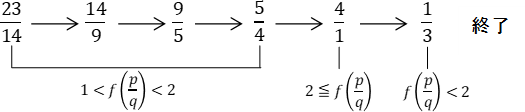
 に対して
に対して を考えたが,
を考えたが,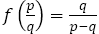 に対してもこの値を考えると
に対してもこの値を考えると となり,プラスマイナスで変化していて絶対値は変わらない。
となり,プラスマイナスで変化していて絶対値は変わらない。
実際,上の例では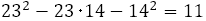
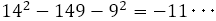
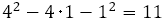
 となり,その絶対値は保たれる。
となり,その絶対値は保たれる。
さて,この操作をもとにいくつかの命題を証明し,下準備をする。
【命題1】
最初に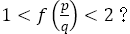 の判断は繰り返されるが,この回数は有限である。
の判断は繰り返されるが,この回数は有限である。
【証明】
最初 であるから,
であるから, である。
である。 であるから次の分数の分母は正である。
であるから次の分数の分母は正である。
また,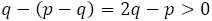 であるので,
であるので,
よって,分母は必ず小さくなる。したがって,この操作は有限回である。
この判断操作を続け,終了した値を考える。その値は2以上であるか,1以下である。
もちろん,そのときの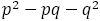 の値も,直前の値にマイナスをかけたものである。
の値も,直前の値にマイナスをかけたものである。
【命題2】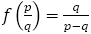 を施して,
を施して,
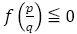 となって終了することはない。
となって終了することはない。
【証明】 のとき
のとき
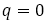 となり,これはあり得ない。
となり,これはあり得ない。
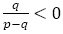 のとき,分子は正なので分母が負。よって,
のとき,分子は正なので分母が負。よって,
よって, の手前の
の手前の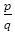 は
は
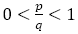 であり,この段階で終了していたはずである。
であり,この段階で終了していたはずである。
よって,あり得ないことが示された。
もし,値が2以上ならばもう一度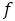 を施すが,施すべき2以上の値に対して場合分けをして考察してみる。
を施すが,施すべき2以上の値に対して場合分けをして考察してみる。
【命題3】 のとき,この操作は
のとき,この操作は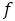 を1回施して終了になる。
を1回施して終了になる。
【証明】
このとき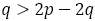 つまり
つまり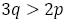
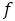 を施すと
を施すと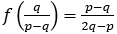
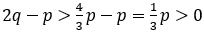 より,分母は正である。また,
より,分母は正である。また,
 により
により
分子<分母になり,
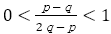 である。よって,
である。よって,
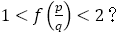 と
と
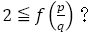 の判断をNoで通り,終了することになる。
の判断をNoで通り,終了することになる。
【命題4】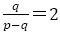 のとき,これはフィボナッチからの分数の流れで
のとき,これはフィボナッチからの分数の流れで
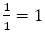 になって終了する。
になって終了する。
【証明】
このとき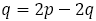 から
から
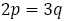
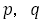 は既約より,
は既約より,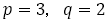
これはフィボナッチの数列からの分数 からの流れである。
からの流れである。
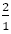 に
に 施され,
施され,
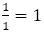 になる。フィボナッチからの分数はここにたどり着き,ここで終了することになる。逆の操作を考えれば,それ以外の分数列が1となってたどり着くことはない。
になる。フィボナッチからの分数はここにたどり着き,ここで終了することになる。逆の操作を考えれば,それ以外の分数列が1となってたどり着くことはない。
以上,すべてこの流れが終了するときには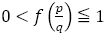 となっている。特に
となっている。特に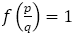 の場合はフィボナッチからの分数のときで,それが
の場合はフィボナッチからの分数のときで,それが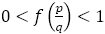 になることはない。
になることはない。
最後に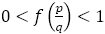 となって終了する列を考える。
となって終了する列を考える。
【命題5】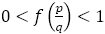 のとき,
のとき,
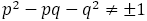 である。
である。
【証明】 のとき,
のとき,
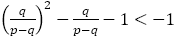 である。
である。
なぜなら,
 において,
において,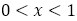 において
において
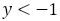 である。よって,
である。よって, とおけばよい。上の不等式の分母を払って,
とおけばよい。上の不等式の分母を払って,
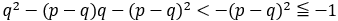
つまり なので,
なので, よって,
よって,
 がいえた。
がいえた。
まとめると手続きが終了した値について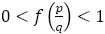 であるか,または
であるか,または
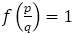 である。前者は
である。前者は である。後者はフィボナッチからの分数列で,
である。後者はフィボナッチからの分数列で,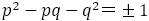 である。よって,次の目標としていた定理がいえたことになる。
である。よって,次の目標としていた定理がいえたことになる。
【定理】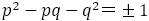 となるのはフィボナッチの数列からの分数のときのみである。
となるのはフィボナッチの数列からの分数のときのみである。
これで長い証明が終了した。
前掲した表で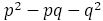 の値をみると,
±2や±3はない。このことはこの後の証明の途中にも使うので,なぜないのか示しておく。
の値をみると,
±2や±3はない。このことはこの後の証明の途中にも使うので,なぜないのか示しておく。
【命題6】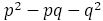 の値は±2になることはない。
の値は±2になることはない。
【証明】
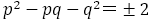 とする。
とする。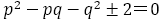
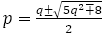 (複合同順)
(複合同順)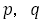 は整数なので
は整数なので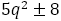 は平方数でなければならない。
は平方数でなければならない。
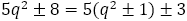 (複合同順)であるが,
(複合同順)であるが,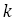 を整数として
を整数として
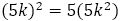
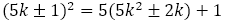
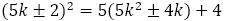 (複合同順)
(複合同順)
となるので, 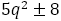 が平方数になることはない。よって,
が平方数になることはない。よって,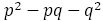 が±2になることはない。
が±2になることはない。
同様の理由で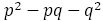 の値が±3になることもない。
の値が±3になることもない。
さらに次のこともいえる。
【命題7】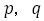 が互いに素ならば,
が互いに素ならば,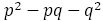 の値は±4になることはない。
の値は±4になることはない。
【証明】
なぜなら,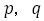 が共に奇数ならば,
が共に奇数ならば,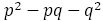 は奇数である。また
は奇数である。また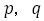 の一方が偶数で,一方が奇数の場合も
の一方が偶数で,一方が奇数の場合も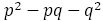 は奇数になる。
は奇数になる。
よって,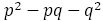 が偶数の場合は,
が偶数の場合は,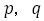 が共に偶数のときである。しかし
が共に偶数のときである。しかし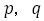 が互いに素なのでこれはあり得ない。よって,証明された。
が互いに素なのでこれはあり得ない。よって,証明された。
命題6,命題7をあわせて,次のことがいえる。
【命題8】 の近似分数
の近似分数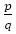 については,
については,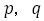 がフィボナッチ数列以外の数で,互いに素であるとき,
がフィボナッチ数列以外の数で,互いに素であるとき,
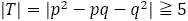 である。
である。
もう1つ,証明して本題の証明に入る。フィボナッチからの分数列について次のことがいえる。
【命題9】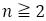 のとき
のとき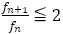 が成り立つ。
が成り立つ。
【証明】 より
より
 は単調に増加するので
は単調に増加するので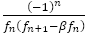 の絶対値は0に近づく。
の絶対値は0に近づく。
また, のとき
のとき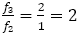
よって,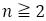 のとき
のとき
よって,証明できた。
さて,以上のことを踏まえて,次の最終的な定理がいえる。
【定理】 と
と の間にある近似既約分数
の間にある近似既約分数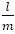 つまり,
つまり,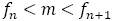 である分母
である分母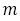 とする近似既約分数において
とする近似既約分数において
 である。
である。
【証明】
命題9より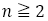 のとき,
のとき,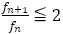
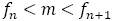 なので,
なので,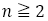 のとき,
のとき,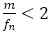 である。
である。
また,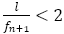 であることを示す。
であることを示す。
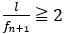 とすると,
とすると,
よって,
よって,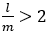
近似値として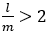 であることはあり得ない。よって,
であることはあり得ない。よって,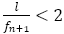
さて命題8より,
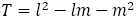
 が成り立つ。
が成り立つ。
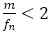
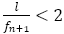 なので,
なので,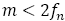

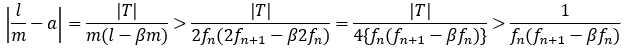
よって,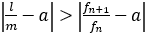
 と
と の間に現れる近似分数
の間に現れる近似分数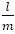 はすべて
はすべて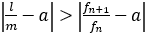 を満たすことがわかる。
を満たすことがわかる。
(証明終了)
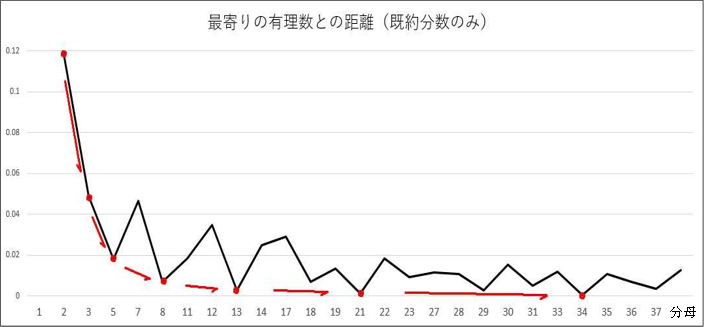
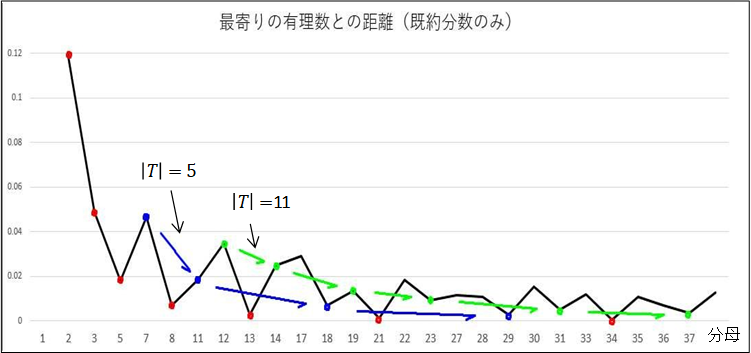
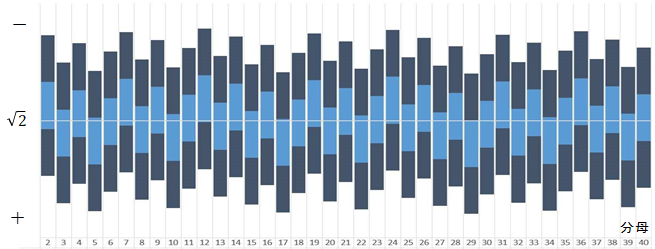
下図はこの定理を視覚的に表したものである。
横軸を分母とし,近似分数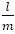 に対して
に対して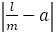 をグラフにしたものである。分母がフィボナッチのときそのときに限り,距離の最小値が更新されているのがわかる。
をグラフにしたものである。分母がフィボナッチのときそのときに限り,距離の最小値が更新されているのがわかる。
換言すれば,フィボナッチからの分数列が に近い最も内側の有理数である。
に近い最も内側の有理数である。
下のグラフは前のグラフに, の場合(青で表示)と
の場合(青で表示)と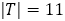 の場合(緑で表示)を表示したものである。
の場合(緑で表示)を表示したものである。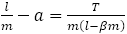 であるので,フィボナッチからの分数に次いで
であるので,フィボナッチからの分数に次いで が,次に
が,次に
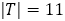 が0に近づくことがわかる。
が0に近づくことがわかる。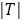 の値が大きいほど,近づくスピードは遅くなる。
の値が大きいほど,近づくスピードは遅くなる。
近似分数を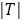 の値ごとに場合分けして表示すると,意外なことに気づいた。
の値ごとに場合分けして表示すると,意外なことに気づいた。
 となる近似分数は以下の通りであるが,すべてが
となる近似分数は以下の通りであるが,すべてが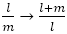 なる操作でつながっている。
なる操作でつながっている。
しかし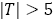 の場合には,
の場合には,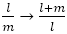 なる操作でつながっている“枝”は 2 本ずつ存在しているようである。これらはこの操作でつながっていない。なぜこのようになるか,次回までの課題としよう。
なる操作でつながっている“枝”は 2 本ずつ存在しているようである。これらはこの操作でつながっていない。なぜこのようになるか,次回までの課題としよう。

ちなみにそれぞれの分数列において,ある程度分母が大きい値から始まっている。たとえば の場合,
の場合, から始まっているが,逆操作によって
から始まっているが,逆操作によって
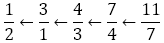
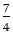 は分母4の分数で最良の近似値ではない。近似値は
は分母4の分数で最良の近似値ではない。近似値は
 である。その意味で,近似値の中に現れていない。
である。その意味で,近似値の中に現れていない。 の分数列の分母2,1,3,4,7,11,18,29・・・はリュカ数である。
の分数列の分母2,1,3,4,7,11,18,29・・・はリュカ数である。 であるのはこの1通りしかない。
であるのはこの1通りしかない。 の分母
の分母
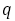 縦軸に分子
縦軸に分子
 を対応させ,
を対応させ,
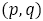 のところに値,
のところに値,
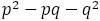 を計算したものがかかれている。特に値が±1と±55のところには色をつけている。±1はもちろんだが,±55も最初は揺れながら,原点からの方向が±1と同じ方向に伸びていることがわかる。その方向の傾きは,後述する
を計算したものがかかれている。特に値が±1と±55のところには色をつけている。±1はもちろんだが,±55も最初は揺れながら,原点からの方向が±1と同じ方向に伸びていることがわかる。その方向の傾きは,後述する
 であり,その下側が負の領域,上側が正の領域になっている。
であり,その下側が負の領域,上側が正の領域になっている。



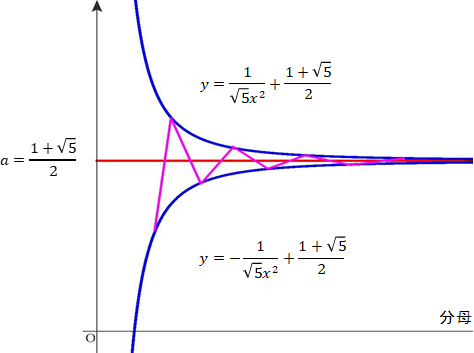
ところで,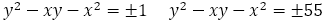 を曲線として描くと右の図のようになる。それぞれ双曲線になっていることがわかる。それらの双曲線の漸近線は,
を曲線として描くと右の図のようになる。それぞれ双曲線になっていることがわかる。それらの双曲線の漸近線は,

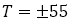 のところは曲線
のところは曲線
 と
と
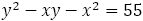 上の点で,これらを行き来している。さらに前述したように
上の点で,これらを行き来している。さらに前述したように
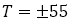 のところは下図のようにすべてが
のところは下図のようにすべてが
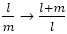 の操作で1つにながっているのではなく,次の図のように,独立した2 本の流れからなっている。しかもそれらは互いに交差している。
の操作で1つにながっているのではなく,次の図のように,独立した2 本の流れからなっている。しかもそれらは互いに交差している。

さてここで が
が
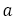 に近づいていく“速さ”を考えよう。ここで“速い”とは,この場合,分母が小さい割に,よい近似値になっているということである。
に近づいていく“速さ”を考えよう。ここで“速い”とは,この場合,分母が小さい割に,よい近似値になっているということである。
前述した式から,
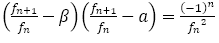

 を限りなく大きくすると
を限りなく大きくすると
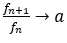 より,
より,

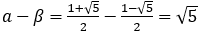 より,
より,
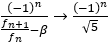
よって, を限りなく大きくすると
を限りなく大きくすると

よって
,
 が十分に大きいとき,
が十分に大きいとき,
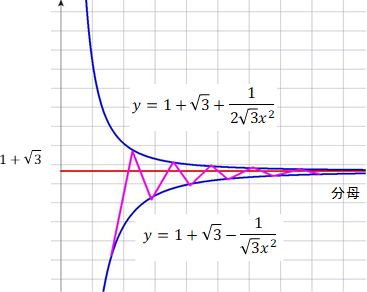
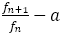 はどんどん0に近づくが,それは分母の2乗に反比例し,その係数は
はどんどん0に近づくが,それは分母の2乗に反比例し,その係数は
 である。次の図はフィボナッチからの分数列が
である。次の図はフィボナッチからの分数列が
 に近づくイメージである。
に近づくイメージである。
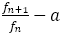 に
に
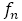 をかけても
をかけても
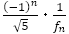 の値に近似しながら0になる。
の値に近似しながら0になる。
しかし,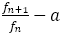 に
に
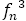 をかけるとその値は発散してしまうこともわかる。
をかけるとその値は発散してしまうこともわかる。
下のグラフは横軸を分母として,
 に分母である
に分母である
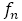 をかけたものである。
をかけたものである。
分母がフィボナッチ数列のとき0に近づいているのがわかる。

フィボナッチからの分数列ではなく,たとえば であるリュカ数からつくられた分数列の場合は,
であるリュカ数からつくられた分数列の場合は,
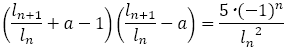
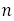 が十分に大きいとき,
が十分に大きいとき,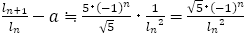
となる。
リュカ数からつくられた分数列の場合も,分母の2 乗に反比例するがその速度はフィボナッチ数列の場合に比べ5倍遅い。
一般にフィボナッチ型の数列の近づく速さは,フィボナッチ数列の場合に比べ, 倍遅くなる。既約分数の場合,
倍遅くなる。既約分数の場合,
 の値は以下の数である。
の値は以下の数である。
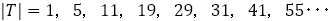
そして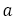 に近づくフィボナッチ型の数列は
に近づくフィボナッチ型の数列は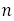 が十分に大きいとき次のものに限る。
が十分に大きいとき次のものに限る。
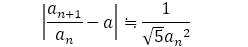
1種類(フィボナッチからの分数)
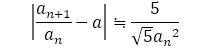
1種類(リュカ数からの分数)
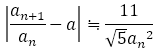
2種類
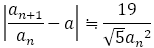
2種類
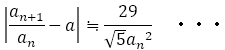
2種類

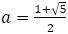 の周りの分数は,その分数の分母に着目すると,
の周りの分数は,その分数の分母に着目すると,
 より大きく
より大きく
 より小さく,
より小さく,
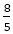 より大きく
より大きく
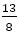 より小さい値である。
より小さい値である。
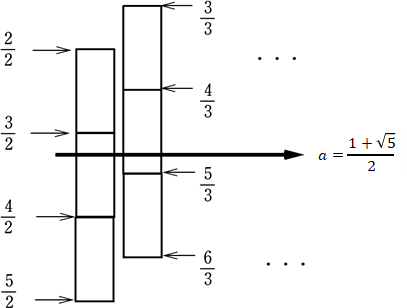
これをイラストしたものが右図である。
フィボナッチ数列以外の分母はここからは隠れて見えない。
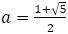 は
は  と
と
 の間を,
の間を,
 と
と
 の間を進んでいくが,それを上から見た図が下図である。わかりやすいように,各分数の間の幅(本来なら縮まるところ)を一定に描いている。
の間を進んでいくが,それを上から見た図が下図である。わかりやすいように,各分数の間の幅(本来なら縮まるところ)を一定に描いている。
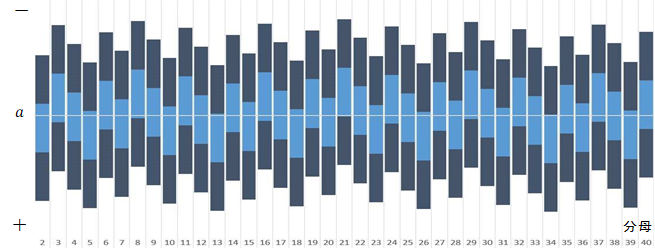
さらに分母を拡張してパソコンで描いたものが下図である。中央の横線である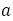 に近接しているところはフィボナッチからの分数列である。
に近接しているところはフィボナッチからの分数列である。
参考までに,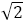 で同様な操作をすると次の下図のようになる。この“模様”は,無理数によって特有なものになる。また
で同様な操作をすると次の下図のようになる。この“模様”は,無理数によって特有なものになる。また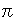 については次頁の図のようになる。
については次頁の図のようになる。
黄金比は連分数で次のように展開できる。
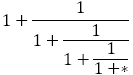
また,
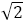 はコンピュータのシュミレーションにもあったように
はコンピュータのシュミレーションにもあったように
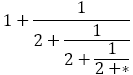
のように展開できる。よって,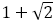 を考えると,
を考えると,
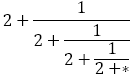
のようになる。整数がすべて2になる。その意味で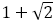 を白銀比と定義する流儀もある。
を白銀比と定義する流儀もある。
この場合,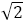 は
は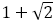 と区別して「大和比」とよばれることがある。
と区別して「大和比」とよばれることがある。
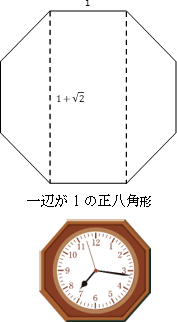
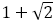 は一辺が1の正八角形の高さに相当し,時計等安定した置物の比にも使われる。
は一辺が1の正八角形の高さに相当し,時計等安定した置物の比にも使われる。
ちなみに,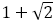 を解に持つ2 次方程式は
を解に持つ2 次方程式は である。
である。
これはまた,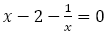 から
から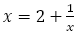
よって,次のように変形されることからも裏付けられる。
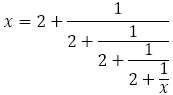
ここから数列を構成していく。


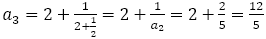
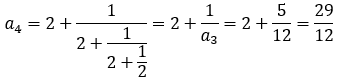
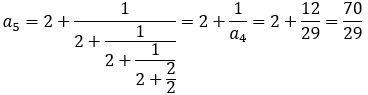
 は
は
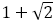 に近づくと思われるが,
に近づくと思われるが,
この数列を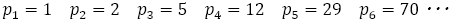 とおくと,
とおくと,
 と表すことができる。
と表すことができる。
連分数のつくり方から,ある項の分子が次の項の分母にまわることは明らかである。
この
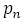 についてみていこう。
についてみていこう。
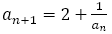 なので,
なので, が成り立つ。ここから,
が成り立つ。ここから,
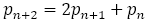 が出てくる。つまりこの数列
が出てくる。つまりこの数列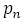 は
は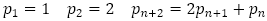 で定まる数列である。
で定まる数列である。
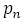 の
の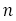 番目の項を式で表す。
番目の項を式で表す。
実は,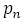 は
は を計算したときの
を計算したときの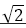 の係数に一致する。つまり
の係数に一致する。つまり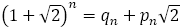 となる。
となる。
なぜなら,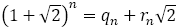 とおけば,
とおけば,
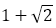 は
は
 の解なので,
の解なので,
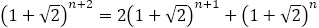
が成り立つ。よって

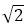 の係数に着目すれば,
の係数に着目すれば,
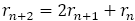 が成り立つことがわかる。
が成り立つことがわかる。
しかも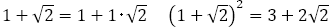 であるから
であるから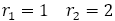 である。
である。
 であったから
であったから
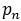 と
と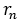 は一致する。
は一致する。
また, であるので,
であるので,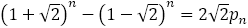 よって,
よって,
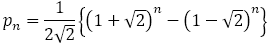
が成り立つ。この数列は「ペル数」とよばれる。
そして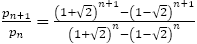 は次の計算から
は次の計算から
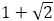 に限りなく近づくことがわかる。
に限りなく近づくことがわかる。
実際,

なので,分母の値は正の値で1に近づき,分子は正負を繰り返しながら0に近づく。
つまり, は
は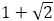 の値より大きくなったり,小さくなったりを繰り返しながら
の値より大きくなったり,小さくなったりを繰り返しながら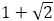 に近づいていく。
に近づいていく。
ところで,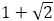 は
は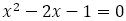 の解である。
の解である。
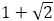 は無理数であり,有理数
は無理数であり,有理数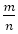 は解にはならないので
は解にはならないので
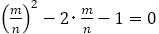 にはならない。
にはならない。
換言すれば,
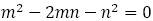 にはならない。
にはならない。
しかし,もし
 であれば,そのような
であれば,そのような
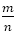 は
は
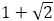 の“よい”近似値であると考えられる。
の“よい”近似値であると考えられる。
先に導いたペル数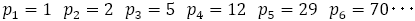 に対して
に対して がこれにあたるかどうかを計算すると,以下のように±1の値になっていることがわかる。
がこれにあたるかどうかを計算すると,以下のように±1の値になっていることがわかる。
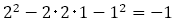
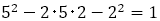

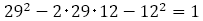

図式化すると次のようになる。

なぜならば, はこの順に白銀比を構成するペル数の途中の項とする。隣接する
はこの順に白銀比を構成するペル数の途中の項とする。隣接する に対して
に対して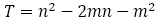 の値を考える。次の隣接する
の値を考える。次の隣接する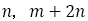 に対して
に対して の値は
の値は
つまり隣接する項で,この値は絶対値は同じで,プラスマイナスを繰り返す。
よって,ペル数では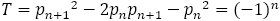 が成り立つ。
が成り立つ。
 は変形すると
は変形すると
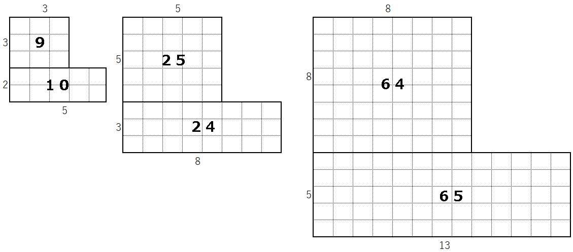
 となり,これを図式化すると,右図の灰色の正方形の面積と,L字型の面積の差が1という解釈になる。次の図でもわかるように,実際に確かめてみると確かに面積の差は1である。しかも正方形の面積の方がL字型に比べて大きくなったり小さくなったりしている。
となり,これを図式化すると,右図の灰色の正方形の面積と,L字型の面積の差が1という解釈になる。次の図でもわかるように,実際に確かめてみると確かに面積の差は1である。しかも正方形の面積の方がL字型に比べて大きくなったり小さくなったりしている。

なお,少し蛇足になるが,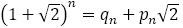 において
において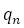 は
は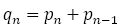 を満たす。ただし,
を満たす。ただし,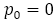 とする。
とする。
なぜなら,

よって, となるからである。
となるからである。
この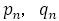 は,
は, を満たす。
を満たす。
実際,
また次の図からも明らかである。

整数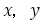 について不定方程式
について不定方程式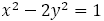 をペル方程式という。(一般に形では平方数でない自然数
をペル方程式という。(一般に形では平方数でない自然数 に対して
に対して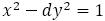 )
)
 はこのペル方程式に解を与える。具体的には
はこのペル方程式に解を与える。具体的には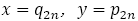 である。
である。
さて,話を元に戻そう。黄金比のときも考えたが,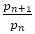 とその次の項
とその次の項 の差について考える。
の差について考える。
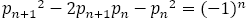 より両辺を
より両辺を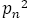 で割ると,
で割ると,
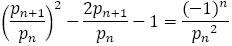 ・・・①
・・・①
一方, は
は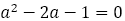 ・・・② を満たす。
・・・② を満たす。
上式で①から②を引くと,
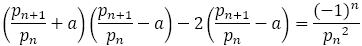
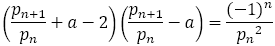
 ただし,
ただし,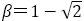
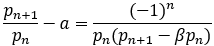
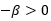 に気をつけると
に気をつけると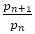 は
は より大きくなったり小さくなったりを繰り返し,
より大きくなったり小さくなったりを繰り返し, に近づく。
に近づく。
さらに,


より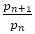 と
と の距離より次の分数
の距離より次の分数 と
と との距離の方が必ず小さくなることがわかる。
との距離の方が必ず小さくなることがわかる。
また次のように変形でき,
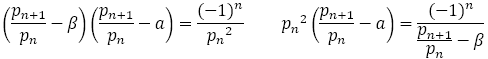
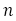 を限りなく大きくすると
を限りなく大きくすると より
より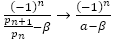
また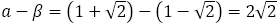 より
より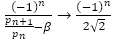
よって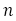 を限りなく大きくすると
を限りなく大きくすると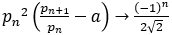 となり,次のことがいえる。
となり,次のことがいえる。
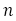 が十分大きいとき
が十分大きいとき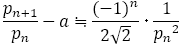
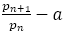 はどんどん0に近づくが,それは分母の2乗に反比例し,その係数は
はどんどん0に近づくが,それは分母の2乗に反比例し,その係数は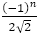 である。
である。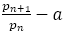 に
に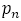 をかけても
をかけても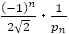 の値に近似しながら0に近づく。
の値に近似しながら0に近づく。
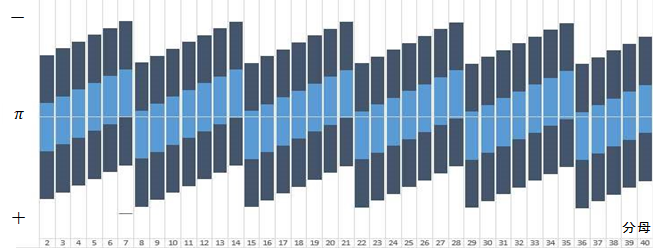
下の表は分母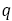 を1から40まで動かして,
を1から40まで動かして, に最も近くなるように,分子
に最も近くなるように,分子 を選んだもので既約分数のみを挙げている。ここで
を選んだもので既約分数のみを挙げている。ここで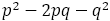 を計算すると,分母がペル数の時に限り±1になっていることがわかる。このことの証明は,黄金比の場合と同様であり,証明もかなり長くなるのでここでは省略する。
を計算すると,分母がペル数の時に限り±1になっていることがわかる。このことの証明は,黄金比の場合と同様であり,証明もかなり長くなるのでここでは省略する。

ここまでは黄金比の場合と類似していることがわかる。しかし,ペル数による白銀比の場合,黄金比の場合と異なるところもある。
黄金比のときは,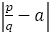 の値が,フィボナッチの数列のときに初めてその最小値が更新された。換言すれば,
の値が,フィボナッチの数列のときに初めてその最小値が更新された。換言すれば,
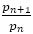 と
と の間に現れる近似分数
の間に現れる近似分数 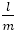 はすべて
はすべて を満たす。
を満たす。
しかし,次の表からペル数に出てこない分母が3と17において最小値が更新されることが確かめられる。このとき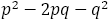 の値は-2である。上の表では大きく□で囲ってある。
の値は-2である。上の表では大きく□で囲ってある。
換言すれば,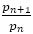 と
と の間に現れる近似分数
の間に現れる近似分数 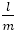 はすべて
はすべて を満たすとは限らない。
を満たすとは限らない。
次の折れ線グラフの青い中が空の円のところが例外である。連分数から漏れた分数であり,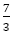 と
と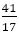 である。この後も現れる可能性がある。ただ
である。この後も現れる可能性がある。ただ のとき,最小値が更新されるかというとそうでもない。
のとき,最小値が更新されるかというとそうでもない。 のときは
のときは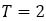 であるが,最小値は更新されない。
であるが,最小値は更新されない。
なぜ連分数から漏れる分数があるかはなぞである。次回への課題としよう。
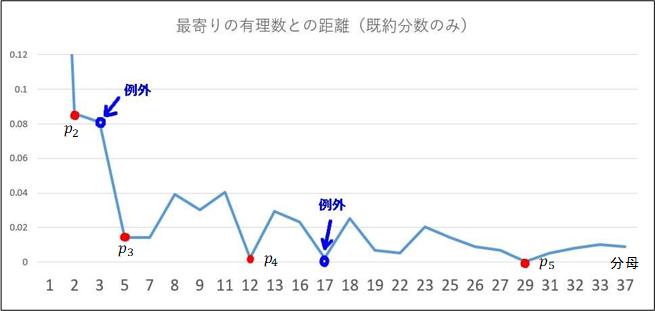
白銀比(ペル数)のみから構成される分数では が成り立つが,分母をスライドさせて,
が成り立つが,分母をスライドさせて,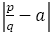 の最小値が更新される数列すべてを入れると,係数
の最小値が更新される数列すべてを入れると,係数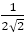 の値はさらに下がるかもしれない。
の値はさらに下がるかもしれない。
同様に と展開できる数は青銅比という。
と展開できる数は青銅比という。
この比の値は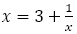 でなければならないので,
でなければならないので,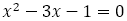 の正の解であり,
の正の解であり,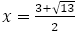 である。
である。
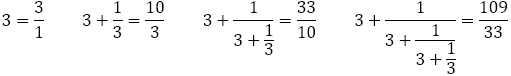
 は
は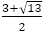 に近づいていく。
に近づいていく。
連分数のつくり方から,分数列の分子が次の項の分母にまわることは明らかである。
この数列を とすると
とすると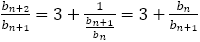
これを変形して数列の分母に現れる1,3,10,33,109・・・の一般項 は,
は,
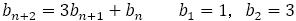
を満たす数列である。
この数列は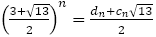 としたときの
としたときの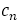 つまり
つまり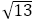 の係数に現れる数に一致する。実際,
の係数に現れる数に一致する。実際,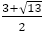 は
は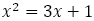 の解であり,
の解であり,
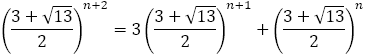
が成り立つから, が成り立つ。
が成り立つ。
また,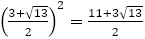 であり,
であり,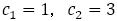 を満たすので,
を満たすので, と
と は一致する。
は一致する。
さらに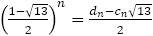 であるので,
であるので,

が導ける。
 が
が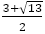 に近づいていくことも以下の計算から確かめられる。
に近づいていくことも以下の計算から確かめられる。
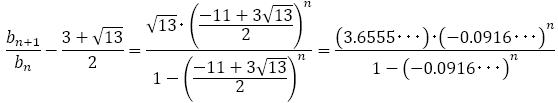
 は
は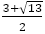 に対して大きくなったり小さくなったりを繰り返しながら近づいていくことがわかる。
に対して大きくなったり小さくなったりを繰り返しながら近づいていくことがわかる。
ところで,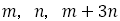 はこの順に青銅比を構成する数列の途中の項とする。
はこの順に青銅比を構成する数列の途中の項とする。
隣接する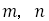 に対して
に対して の値を考える。次の隣接する
の値を考える。次の隣接する に対して
に対して の値は,
の値は,
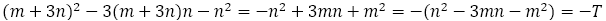
つまり隣接する項で,この値は絶対値は同じで,プラスマイナスを繰り返す。実際,この青銅比からの数列で最初から計算すると,

よって,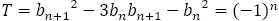 が成り立つ。
が成り立つ。
よって,両辺を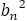 で割ると,
で割ると,
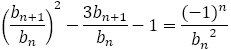 ・・・①
・・・①
一方, は
は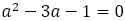 ・・・②を満たす。
・・・②を満たす。
上式で①から②を引いて,黄金比や白銀比と同様に計算すると,
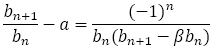 ただし,
ただし, を得る。
を得る。
 に気をつけると
に気をつけると は
は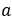 より大きくなったり小さくなったりを繰り返し,
より大きくなったり小さくなったりを繰り返し,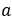 に近づく。
に近づく。
さらに であり,
であり,
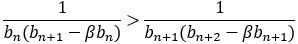
であるので, と
と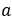 の距離より次の分数
の距離より次の分数 と
と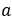 との距離の方が必ず小さくなることがわかる。
との距離の方が必ず小さくなることがわかる。
 が青銅比に近づく速さ
が青銅比に近づく速さ
ところで,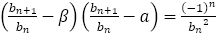 から
から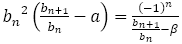
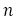 を限りなく大きくすると
を限りなく大きくすると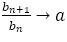 より
より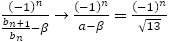
よって,黄金比や白銀比と同様に計算して次のことがいえる。
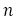 が十分大きいとき
が十分大きいとき
 はどんどん0に近づくが,それは分母の2乗に反比例し,その係数は
はどんどん0に近づくが,それは分母の2乗に反比例し,その係数は である。
である。
 に
に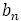 をかけても
をかけても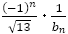 の値に近似しながら0になる。
の値に近似しながら0になる。
下の表は分母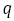 を1から40まで動かして,
を1から40まで動かして,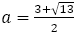 に最も近くなるように,分子
に最も近くなるように,分子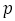 を選んだもので既約分数のみを挙げている。
を選んだもので既約分数のみを挙げている。

ここで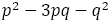 を計算すると,分母がこの数列のときに限り±1になっていることがわかる。このことの証明は,黄金比や白銀比の場合と同様に,証明もかなり長くなるのでここでは省略する。
を計算すると,分母がこの数列のときに限り±1になっていることがわかる。このことの証明は,黄金比や白銀比の場合と同様に,証明もかなり長くなるのでここでは省略する。
ここまでは白銀比と同様に黄金比の場合と類似していることがわかる。しかし,ここでも青銅比を構成する分数の場合,黄金比の場合と異なるところがでてくる。
黄金比のときは,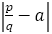 の値が,フィボナッチの数列のときに初めてその最小値が更新された。
の値が,フィボナッチの数列のときに初めてその最小値が更新された。
しかし,下のグラフからは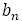 に出てこない分母が2と7と23のときも最小値が更新されることが確かめられる。
に出てこない分母が2と7と23のときも最小値が更新されることが確かめられる。
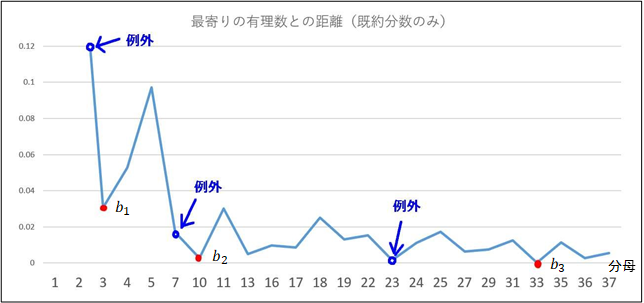
このときの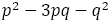 の値は±3である。前の折れ線グラフの青い中が空の円のところが例外である。
の値は±3である。前の折れ線グラフの青い中が空の円のところが例外である。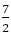 と
と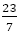 と
と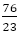 である。
である。
換言すれば,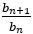 と
と の間に現れる近似分数
の間に現れる近似分数 はすべて
はすべて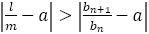 を満たすとは限らない。
を満たすとは限らない。
これも白銀比のときと同様になぞである。次回への課題としよう。
ところで,青銅比のみから構成される分数では,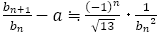 が成り立つが,分母をスライドさせて,
が成り立つが,分母をスライドさせて, の最小値が更新される数列すべてを入れると,係数
の最小値が更新される数列すべてを入れると,係数 の値はさらに下がるかもしれない。
の値はさらに下がるかもしれない。
この青銅比は現実の世界ではあまり使用されていないようだが,例えば,横長の窓や壁の全体を活用した掲示やデザイン等を考える場合に1つの参考比率となっているようである。またホームページ作成で,ウィンドウ幅いっぱいのメインビジュアル(トップページのヘッダーの下に表示出来る画像)の高さを決める時など,参考にするようである。
これまで,黄金比をはじめ,白銀比,青銅比をみてきた。
| 黄金比 | 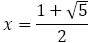 |
 |
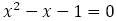 の正の解 の正の解 |
| 白銀比 | 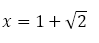 |
 |
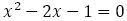 の正の解 の正の解 |
| 青銅比 |  |
 |
 の正の解 の正の解 |
一般に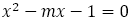 の正の解は
の正の解は であり,その連分数は
であり,その連分数は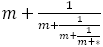 表される。これらの比のことを「第
表される。これらの比のことを「第 貴金属比」という。
貴金属比」という。
第1貴金属比は黄金比,第2貴金属比は白銀比,第3貴金属比は青銅比にあたる。
第 貴金属比を連分数から構成する数列は,
貴金属比を連分数から構成する数列は,
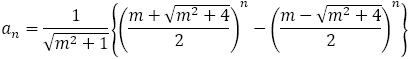
であり, は
は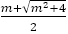 に近づいていく。よって次のことがいえる。
に近づいていく。よって次のことがいえる。
 が十分大きいとき
が十分大きいとき
いずれの場合も,数列と,その数列が近づく値の距離は,数列の分母の2乗に反比例する。そのときの係数は,
黄金比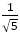 白銀比
白銀比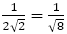 青銅比
青銅比 で,この後も小さくなるばかりである。この値は黄金比が一番大きい。
で,この後も小さくなるばかりである。この値は黄金比が一番大きい。
その意味で,黄金比はこの中で,有理数と一番距離を取っている無理数であることが裏付けられる。そして黄金比と一番近い距離にある有理数はフィボナッチから構成された分数である。
ところで,これまで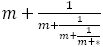 といった,すべて出てくる値が同じ連分数のものを考えたが,数によって連分数にでてくる数字は当然何種類もでてくる場合もある。たとえば,
といった,すべて出てくる値が同じ連分数のものを考えたが,数によって連分数にでてくる数字は当然何種類もでてくる場合もある。たとえば,
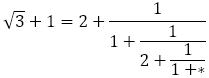
と連分数展開できる。ここからでてくる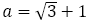 に近づく数列は
に近づく数列は
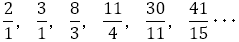
である。この数列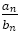 に対して,
に対して,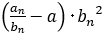 がどう変化するかを考える。
がどう変化するかを考える。
途中計算は省略するが,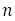 が十分大きい数のとき,
が十分大きい数のとき,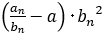 は次のようになる。
は次のようになる。
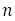 が奇数のとき
が奇数のとき
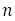 が偶数のとき
が偶数のとき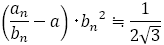
つまり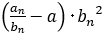 は偶数と奇数の項で近づく値が異なる。しかし今は
は偶数と奇数の項で近づく値が異なる。しかし今は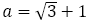 とその周りの有理数との距離を考えているので,距離が狭い方を考えるのが妥当であろう。したがって次のことがいえる。
とその周りの有理数との距離を考えているので,距離が狭い方を考えるのが妥当であろう。したがって次のことがいえる。
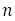 が十分大きいとき
が十分大きいとき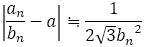
いずれにしても,黄金比のときは,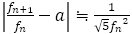 であったので,黄金比に比べて有理数が密着していることがわかる。
であったので,黄金比に比べて有理数が密着していることがわかる。
数列が に近づいていくイメージ
に近づいていくイメージ
下の曲線の方が から離れている
から離れている
一般に と連分数展開できる数
と連分数展開できる数 に対して,そこに近づく分数
に対して,そこに近づく分数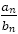 の列を連分数からつくったとき,次のことがいえる。これも長い計算が必要なので途中を省略する。
の列を連分数からつくったとき,次のことがいえる。これも長い計算が必要なので途中を省略する。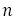 が十分大きいとき,
が十分大きいとき,
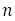 が奇数のとき
が奇数のとき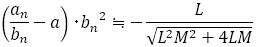
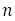 が偶数のとき
が偶数のとき
よって,この場合も偶数と奇数の項で近づく値が異なり,有理数との距離は狭い方をとって,
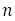 が十分大きいとき
が十分大きいとき
がいえる。仮に の方が小さいとして
の方が小さいとして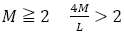 であるから,
であるから,
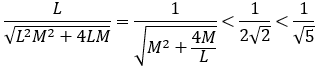
が成り立ち,黄金比はもちろん,白銀比と比べても有理数に近く,より密着していることがわかる。
これまで,黄金比のほかに白銀比や青銅比について考えてきた。しかしながら自然界に現れるのは,白銀比でもなく,青銅比でもなく,黄金比である。仮に白銀比が現れるならば,その連分数から導かれる比から導かれる数列1,2,5,12,29,70,169・・・が自然界の中に現れるはずが,今のところ見つからない。
また数学的見地から黄金比の周りの有理数を考えると,その最も内側は,フィボナッチ数列による分数列で出来ており,その内側は“空洞”で有理数は存在しない。その空洞の半径は,他のどの無理数よりも大きいのである。そしてこれが自然界に黄金比が現れる原因になっている。
個人的な見解であるが,生物が進化の過程で偶然黄金比になったとは思えない。何か神秘的なものを感じ,自然を造った創造者の存在に思いをはせる。
約4時間の講座の後,生徒に感想を書いてもらった。以下にその抜粋を載せる。なお,この後,希望者4名に対して(16)以降の内容についてより詳しく説明している。

○今回の講義を受ける前までは黄金比は人間が考えた美しい比率だと思い込んでいました。ところが自然界にはたくさんの黄金比が存在していてハヤブサや蜂の飛ぶ軌跡や葉の付き方など,自然において最も合理的な比率であると聞き,とっても神秘的で美しいと思いました。

○自分は高校に入って数学に興味を持った。自分が興味を持った数学がまさかここまで深い学問だとは想像もしておらず驚いた。講義ついての感想は「フィボナッチ数列」という言葉は前々から聞いたことはあった。自分は「なんかの数が規則的に並んでいるだけじゃないか」と思っていたが,全然そんなものではなく,奥が深い数列だと思った。これからも数学を楽しんでいきたい。

○ という数にあまりなじみはなかったが,この講話を聞いて黄金比に関心を持った。なぜ黄金比が自然界で深く関わりがあるのかが解明されたら,さらに様々なことが解明されていきそうなので,期待したい。今回の講話を開いていただきありがとうございました。
という数にあまりなじみはなかったが,この講話を聞いて黄金比に関心を持った。なぜ黄金比が自然界で深く関わりがあるのかが解明されたら,さらに様々なことが解明されていきそうなので,期待したい。今回の講話を開いていただきありがとうございました。
○以前「数」は単に個数や長さを表すだけのものだと考えていた。有理数,無理数も正直のところ,人間が区別しているだけで,自然界においては大差ないと思っていた。しかし有理数を寄せ付けない黄金比には,葉が重なりにくい等,有理数にはない点があり驚いた。今まで思っていた「数学」とはまた違った数学の見方に気づけました。数学の分野に興味がとてもわいてくる授業をありがとうございました。
○まず第1に数学と自然界の生態系が結びついているということに驚きました。そして「黄金比」の他に「白銀比」,「青銅比」という貴金属比というものがあるということを初めて知りました。また松ぼっくりの螺旋というものは,一般における連分数とは逆に巻いていることが,驚きと疑問にあふれました。地球が誕生してから何億年も経っており,そこにおける生態系の「おもしろさ」というものを学ぶことができました。
○今回講義を受けてみて,数学の意味を,自然と結びつけることで,とても強く感じたと思う。そして今回言っていた内容は,かみ砕いたりしたものであるだろうけども,想像以上に簡単な感じの法則的なものがあるのだと,感動すると共に,これを見つけ出す人たちの見いだす植物,世界などの何とも言えない不思議な神秘的なものが良いなと思う。
○黄金比というものが,この世に存在していることは知っていたが,実際にどういうものなのか理解できず,この講義を受けさせてもらいました。黄金比が自然界の様々な場所にあることがわかり,またそれを数学的に解説してもらえたのが,とても面白くためになりました。
○私たちが日頃過ごしている中でも,多くの比が関係していることがわかった。また私たちの身近にだけではなく,様々な図形や歴史的な建築物,自然界にも幅広く活用されていることがわかった。そして今回の講義を受けて,黄金比とフィボナッチ数列の関係性,連分数の関係性などを理解することができ,黄金比に対しての視覚的美しさだけではなく,数学的美しさを感じることができた。
初めに述べたように,この資料は高校生でも理解できるように,できるだけ簡潔に平易に書いたつもりである。黄金比は昔から多くの方が研究されているので,本稿には真新しいものはないのかもしれない。しかし,他の解説よりも,できるだけ証明の方法を独創的に,しかしわかりやすく工夫したつもりである。
例えば,正五角形の作図のところでも,教科書でのやりかたとは異なったものを考案し紹介している。ちなみに,教科書のやり方は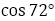 の値を知っていることが前提である。
の値を知っていることが前提である。
また,フィボナッチの数列のところでも,3項間の漸化式から,あの複雑な漸化式の変形を通りがちであるが,そうした知識がなくても一般項を出せるように工夫した。さらに,黄金比の周りの有理数の分布を論じる際にも,黄金比に近づく数列をフィボナッチ数列の一般項から表して考察しがちであるが,そうすると,式の計算が複雑で膨大になり,証明も煩雑になってしまう。本稿では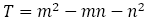 という新しい概念を導入しそれを避けている。
という新しい概念を導入しそれを避けている。
こうして,本稿では様々な数学的事実を明らかにしているが,研究を進む中で,またいくつかのわからない事も出てきている。たとえば,黄金比に近づく数列で, を満たす数列は,2種類あることが見いだされている。また,白銀比や青銅比に近づく数列で,連分数展開から漏れる数列,つまり,白銀比や青銅比に近い数であっても,連分数から導き出せない数も見いだされている。研究をしていく際,新しいことがわかる一方で,その先にまたわからないことが見えてくることは,多くの研究の中で見いだされている。それが次の研究へ向かうバネになることも確かである。本稿ではそうした経験もできる。
を満たす数列は,2種類あることが見いだされている。また,白銀比や青銅比に近づく数列で,連分数展開から漏れる数列,つまり,白銀比や青銅比に近い数であっても,連分数から導き出せない数も見いだされている。研究をしていく際,新しいことがわかる一方で,その先にまたわからないことが見えてくることは,多くの研究の中で見いだされている。それが次の研究へ向かうバネになることも確かである。本稿ではそうした経験もできる。
講義の後,生徒は口々に「深い!」と言っていた。1つのテーマを決めて何時間もかけて突き詰める経験は,普段の授業ではできない。しかしそのような経験により,生徒は数学の奥深さや面白さ,自然等他の事象とのつながりについて学習し,感動につながっている。SSHの数学講座だからこそできる技である。
普段の授業では限られた時間の中で単元の内容を要点をつまんで話をし,そして単元テストを行う。そして次の単元へと移っていく。生徒はこうしたサイクルを何年もの間経験しており,それが数学だと思っている。数学のうわべだけを,“短時間で飛行遊覧して終わっている”と言っても過言ではないであろう。
それなので,生徒に何も教えないでいきなり「黄金比について研究しなさい」と言っても生徒は何をしてよいか戸惑うだけである。この教材は「数学を研究していくということは,こういうことだ!」という1つの模範を示している。単に「上から見下ろして終わり」ではなく,「その地を歩き,土壌を掘り起こしていく」作業をすることが研究なのだということを生徒に知ってもらいたいのである。そしてそこにまで行って初めてわかる数学の価値も感じてほしい。
今後ともこのような機会を設けて生徒に数学で掘り下げることを経験させ,数学観の育成に寄与していきたい。
数年後,生徒達は大学に進学し,様々なことを研究するであろう。ここで学んだ経験が,それぞれの研究の羅針盤として役だってほしいと願っている。
最後に本稿で取り扱った比についてまとめる。長方形の縦は1で,横がそれぞれの比である。
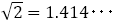 |
白銀比(大和比) |  |
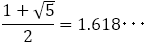 |
黄金比(第1貴金属比) |  |
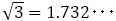 |
プラチナ(白金)比 |  |
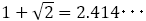 |
白銀比(第2貴金属比) |  |
 |
第2黄金比 |  |
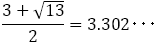 |
青銅比(第3貴金属比) |  |