５．指導の系統化及び価値

(1)	平行線の性質を使って角を移すこと 　この性質の論証で，対頂角，平行などを使って説明するわけであるが， ・ 直線ｍと直線ｎによってつくられるｂを，直線ｎに沿って平行移動し，となるような考え方 ・ ＡＢの中点Ｏを中心にして，180回転してｃとｄが重なるという考え方 など，回す，ずらす，重ねるという直観的操作を大切にした指導をする。
(2)	三角形の内角の和 三角形の内角の和は180である。 1) 　平行線の性質より，１点に３つの角を集める場合 ア イ 2) 　回転の考え方を使う場合 ア イ 3) 　極限の考え方を使う場合
(3)	三角形の外角の和 三角形の１つの外角は，その隣にない２つの内角の和に等しい。 1)　(2)の1)，アの証明の裏返しより 2)　回転の考え方の場合
(4)	ｎ角形の内角の和 ｎ角形の内角の和は，180×(ｎ−２)である。 四角形の場合 1)　頂点に１点を取る場合 2)　内部に１点を取る場合 3)　辺上に１点を取る場合 4)　外部の１点を取る場合 5)　回転角の考え方を使う場合 6)　極限の考え方を使う場合
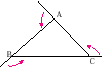
(5)	ｎ角形の外角の和 ｎ角形の外角の和は，360である。 ←・三角形，四角形より類推する。 1)　３か所の平角から内角を除く場合 2)　回転角の考え方を使う場合 1) 2)
(6)	星形五角形の各頂点の角(本時) 　星形五角形の各頂点の角の和は，180である。 　この学習は，具体的操作を通して多様な証明の仕方がわかり，三角形の内角の和，内角と外角の関係，角を１か所に集めること等のアイディアに気がつかなければならない。 　したがって，本単元の核となる学習内容は，１つの図形に対して多様な見方や考え方ができるように，集める，回す，ずらす，重ねるという基本的操作を繰り返すことである。 　即ち，既有の知識を常に統合し，これを組織化し，体系だてるとともに，既有の知識全体に対する見通しを持って，数学が生成発展していく姿を感じとらせなければならない。そのために，本単元を構成するにあたり，次の２点を骨子にした。 ・ 学習の対象を生徒にとって最もなじむ角度から取り上げ，関連のある既有経験を明らかにした上で，その解決に必要とされる知識を明らかにする。 ・ 学習の望ましい姿の１つであるオープン・エンド・アプローチの流れをその学習に具備させる。