この単元では，除数が分数である場合の除法の意味と計算の方法について理解することをねらいとしている。一般的には，分数でわることの意味理解は，分数÷整数の場合を基に，言葉の式に当てはめたり，数直線に表したりして指導を行っている。しかし，計算はできても，除法の意味を正しくとらえることが難しい。そこで，教科書の展開とは異なるが，除法の場がとらえやすい包含除で導入し，式の意味が理解できた後で計算方法を考えていくことにした。

(1) 分数でわることの意味を理解させる教材の工夫

問題

mのテープをmずつ切ります。何本できますか

テープを同じ長さずつ切り分けるという包含除の場面を提示することで，立式が容易になり，分数÷分数の意味が理解しやすくなる。また，長さを扱うことで，小数や整数（cm）で考えることができ，答えの確かめもできる。

(2) 計算の方法を考え，見つけ出すための手立ての工夫

立式後，具体物を使って答えの確認をした後，ここでは結果から分数の計算の方法を考えさせる。面積図や除法の性質をいかした計算方法は次時に扱うようにする。

テープを分ける活動を通して，分数でわることの意味が分かり，計算方法を考え出すことができる。

学習活動		発問と子どもの反応・指導のポイント
1	テープの長さを予想する。 （紙テープ60cmを提示する）	Ｔ テープの長さはどれくらいでしょう。 Ｃ 1mより短いと思います。 Ｃ 50cmぐらいです。 Ｔ 正解は，（mと書く）です。 Ｃ 小数で表すと0.6mです。 Ｃ cmに直すと60cmになります。 テープの長さを与えるのではなく予想させることで，量感をもたせ，分数を小数や整数（cm）に直して考えようとする見方を育てておく。
2	本時の課題を知り，式に表す。 問題 mのテープをmずつ切ります。何本できますか。	Ｔ （問題文を提示）式はどうなるかな。 Ｃ です。 Ｃ えっ分数÷分数ってあるのかな。 Ｃ あると思う。だってmずつ切ると書いてあるから。 Ｃ たとえば4mのテープを2mずつ切るときも，4÷2になります。 テープを同じ長さに切り取るということから整数や小数と同じように分数でもわることができることに気づかせ，立式させる。
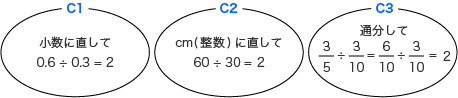
3	自分なりの方法で答えを出す。	Ｔ 答えを出してみよう。 Ｃ みんな答えが2本になりました。 Ｔ （mのテープを提示）本当に2本になるかどうか確かめてみよう。 Ｃ （重ねてみる）2本になりました。 既習事項を活用し答えを出した後に，実際のテープを使って答えを確かめさせる。
4	から計算方法を考える。	Ｔ どのように計算したか考えよう。 Ｃ 難しいな。 Ｔ のの部分を考えてみよう。 途中の計算方法を考えやすいように，手立て2の式を提示し，その部分を考えさせる。形式的に計算方法を知っている児童には，なぜそうなるのかを考えさせるようにする。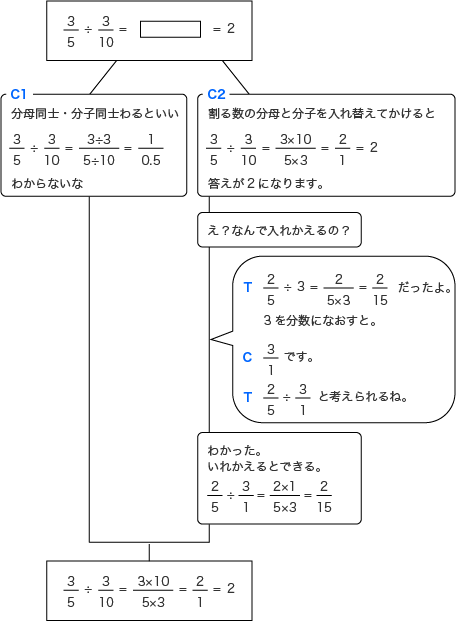
5	計算の方法を知る。	Ｔ 分数÷分数はわる数の分母と分子を入れ替えてかけると答えがわかるね。 分数÷整数の方法に気づかない場合には，教師から分数÷整数の式を提示し，考えを引き出す。 計算の方法は結果から導いたが，わり算の性質を使った計算方法については，次時に取り扱う。
6	問2を解く。 問題 LのジュースをLずつ分けます。いくつに分けられますか。	Ｔ 問2をやってみよう。 Ｃ 式はになります。 Ｃ 計算のやり方はです。 Ｔ 本当になったか確かめてみよう。 事象をかさにかえても，1つのかさを同じ数ずつ分けることからわり算になることを知らせ，解決させる。その後，計算の方法が正しかったかを，液量図を使って確認する。
7	計算練習をする。	本時では分数でわることの意味理解が中心だが，簡単な練習をすることで計算できる喜びをもたせる。
8	学習のまとめをする。	Ｔ 今日の学習でどんなことがわかりましたか。 Ｃ 分数÷分数もあることがわかりました。 Ｃ 計算のやり方は，わる数の分母と分子を入れ替えてかけるといいとわかりました。でも，なんで分母と分子を入れ替えると計算ができるか，よくわかりません。 Ｔ 次の時間に，みんなで考えていきましょう。 児童の言葉でまとめ，児童の疑問を次時にいかすようにする。

(1)　「テープを同じ長さずつ切り分ける」という包含除の問題を扱うことで，「分数÷分数」が成り立つことがわかり，小数や整数などの既習事項を使って，課題を解決することができた。

(2)　計算の方法を考える場面では，先に答えを確認していたため，分数×分数や分数÷整数の計算と関連付けて考える姿が見られた。

(3)　導入の段階では包含除の場面を用いたが，次時以降は，単位量当たりの考えを使った立式や計算の性質を使った計算の仕方について指導していく必要がある。