演算の意味と形式不易の原理
算数の問題解決の中には,意味を保持しようとすると形式が崩れ,形式を保持しようとするとこれまで持ち合わせていた意味に矛盾をきたすという場合がときどきあります。一般にこのような場面では,これまで持ち合わせていた意味を見直し,形式を整えていくのが常であり,これを数学の舞台では形式不易の原理といっています。
例えば,本学年で学習する小数のかけ算ですが,かけ算の導入段階(第2学年)では,「基準量×いくつ分」という形で意味づけがはかられ,その結果を累加で求めています。しかし,乗数が小数になるとその形式がうまく通用しません。下記のような問題で「80円を2.3回たす」ことなど考えられないからです。
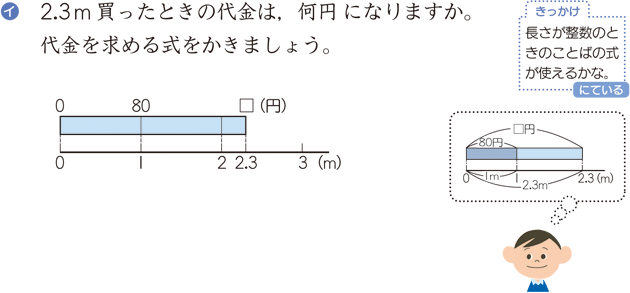
そこで,どうするかといえば,まず数量の関係を右のような数直線図で表し,
2m…80×2
3m…80×3

として,リボンの長さに比例して代金がきまることに着目させ,乗数が小数の場合でも適用できることをおさえるわけです。その背景には,「基準量×いくつ分」から「基準量×測定値」という意味の変換が込められています。
その意味の変換を児童にわかる形で示していくのが,次の「ことばの式」を仲介にした見直しです。
1mのねだん×長さ=代金
これによって,長さが小数の場合でも整数と同様に演算決定ができることをおさえていくわけです。
小数の除法についても,同じような考えで展開をはかっています。