四則に関して成り立つ性質

四則に関して成り立つ性質という場合，基本的に次の２つの内容を指しています。
一つは，計算を支える次のような法則で，いわゆる計算の法則と称されているものであり，もう一つは，たし算やひき算，かけ算，わり算に関して成り立つ性質です。

計算法則は，次の通りです。

１交換法則
■＋●＝●＋■ (加法の交換法則)
■×●＝●×■ (乗法の交換法則)

２結合法則
(■＋●)＋▲＝■＋(●＋▲) (加法)
(■×●)×▲＝■×(●×▲) (乗法)

３分配法則
(■＋●)×▲＝■×▲＋●×▲
(■－●)×▲＝■×▲－●×▲

第４学年では，これまでの整数の計算をもとにしながら，基本となるこれらの計算法則をまとめることになっています。
一方，計算に関して成り立つものとして，第４学年で「除数，被除数に同じ数をかけても，同じ数でわっても商は変わらない」性質が新たに扱われます。

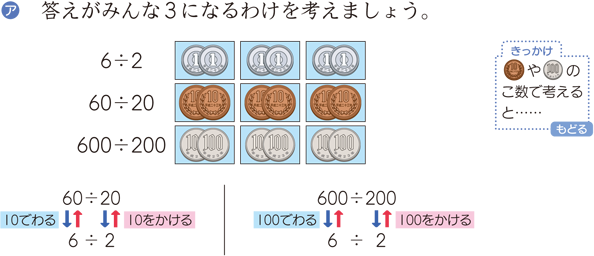
計算の法則にしろ，除法に関して成り立つ性質にしろ，単に形式的にそれらのきまりを指導していては，そのよさもおもしろさも感得できません。
具体的な事象に照らしたり，次のように，計算のくふうと関連づけたりして，それらのよさを明らかにすることが，何よりも大切です。

ア. ４５＋９２＋８＝４５＋(９２＋８)
イ. ２５×３６→２５×(４×９)＝(２５×４)×９
ウ. ９９×５６→(１００－１)×５６＝１００×５６－１×５６