
|
多様な考えを生かす算数科学習指導 〜方向性を明確にした交流活動を通して〜 |
||
|
|||
|
1.はじめに 算数の授業中,子どもたちがいろいろな考えや解決方法を見出しているのに,うまく交流の場を仕組むことできず,活発な交流ができなかったり,とらえるべき内容が曖昧になったりしたことがよくありました。そこで,子どもたちの多様な考えを生かし数理を自ら見出させるために,方向性を明確にした交流活動を仕組み実践することにしました。2.方向性を明確にした交流活動について 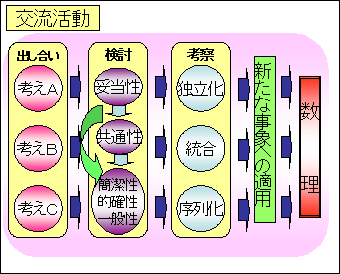 交流活動に入る前,子どもたちは見通しに沿って多様な考えを見出している。それを出し合い,それぞれの考えを検討し,自分の考えを確かにしたり,友達の考えを生かしたりして,より価値ある考えへと高め,数理を見出させていく必要がある。 交流活動に入る前,子どもたちは見通しに沿って多様な考えを見出している。それを出し合い,それぞれの考えを検討し,自分の考えを確かにしたり,友達の考えを生かしたりして,より価値ある考えへと高め,数理を見出させていく必要がある。そこで右図のように3つのパターンに分類し,交流活動を仕組む。それぞれの考えに関連がある場合は考えを統合したり,考えに序列がある場合は序列化し,よりよい考えを選択したり,それぞれの考えが独立している場合それぞれの価値のよさを認めさせたりする。このように,教師が内容をしっかりとらえそれに合った観点で比較検討させることで,多様な考えの価値を高めることできると考える。 3.方向性の違いによる交流活動の3つのパターン
4.方向性を明確にした交流活動の指導の実際
5.終わりに 交流活動を仕組む際に,統合化,序列化,独立化のどのパターンかをとらえるべき内容に応じて見極め,それに応じて観点を明確にして比較検討させことで,子どもたちが見出した多様な考えが生かされ,子どもが考えを高め合って,価値ある考えとして数理を見出すことができたように考える。 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
 |
|
 ○統合化へ向かう交流活動
○統合化へ向かう交流活動 ○序列化へ向かう交流活動
○序列化へ向かう交流活動 ○独立化へ向かう交流活動
○独立化へ向かう交流活動

