| 1) |
子どもの側に立った学習課題の提示(課題の明確化)
学習のねらいを達成するために,本時はどのような内容の学習をするのかを明確にすることを心がけた。特に,子どもの表現でかつ具体的な数字の入った課題,つまり,子どもの側に立った学習課題で提示できるよう工夫した。

T
|  , , , , の分数があります。これらの分数を見て気がつくことはありませんか。 の分数があります。これらの分数を見て気がつくことはありませんか。
|
C1
| 分子はちがうけど,分母が同じです。分母が4になっています。
|
| T | 今日は分母の同じ3つの分数の大きさをくらべようと思います。どれがいちばん大きいでしょうか。 |
|
C2
| 分子が大きいから が大きいと思います。 が大きいと思います。
|

C3
|  は4つに分けた1つ, は4つに分けた1つ, は は が3つ, が3つ, は5つだから一番大きいと思います。 は5つだから一番大きいと思います。
|
T
|  の個数でくらべるわけですね。すごいね。 の個数でくらべるわけですね。すごいね。
|
| T | 他の方法で大きさくらべができないだろうか。
|
C4
| 図,線分図や数直線でできそうです。テープ図も使えるかな。
|
学習課題
 , , , , の分数の大きさを線分図や数直線などに表して,くらべ方を考えよう。(説明しよう) の分数の大きさを線分図や数直線などに表して,くらべ方を考えよう。(説明しよう)
|

|
| 2) |
評価問題での相互交流活動(教え合い,学び合い)
授業の終末で必ず評価問題を提示し解決する活動を位置づけている。この時間は,指導者の側から考えれば本時の学習の理解を評価する場であり,学ぶ側からすれば本時で学んだ考え方の活用の場であるといえる。
子どもたちは一応の解決が終わると,個々に相互交流しながら解決方法や結果の検討を行う。その間,教師は,解決に困っている子どもに対してきめ細かな個別指導を行うことができる。この場面において,「もし, (分子が同じ) , ,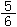 , , の分数だったら大きさはどうだろう。」といった子どもたちの興味・関心の方向としての発展的な学習が導かれ,問題意識となり,話し合われることとなった。 の分数だったら大きさはどうだろう。」といった子どもたちの興味・関心の方向としての発展的な学習が導かれ,問題意識となり,話し合われることとなった。
 
<子どもの興味・関心の方向として次のような学習が展開された>(概要)
 と と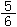 はどちらが大きいだろうか。(分子が同じ分数の大小は?) はどちらが大きいだろうか。(分子が同じ分数の大小は?)
|
C
| 線分図や数直線で表してみると分かる。
| 
|

C
|  は は が5つ, が5つ,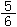 は は が5つだから, が5つだから, と と をくらべればいい。 をくらべればいい。
|

C
| 2本の線分図にしてみると のほうが のほうが より大きい。 より大きい。
|

C
| 一本の数直線にすると の方が大きい。 の方が大きい。
|

C
|  は1より大きい。でも, は1より大きい。でも,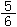 は1より小さい。だから, は1より小さい。だから, の方が大きい。 の方が大きい。
|
|
| 3) |
単元終了後のまとめ「算数“きいて!!”」(学習内容の再構成)
 単元が終わるごとに振り返ってまとめをする活動を位置づけた。この活動では,学習内容の再構成をし,学んだことを結びつけ,関連づけて考えることで理解を確かにしていこうとするものである。右の子どもの「算数“きいて!!”」に見られるように,分数の大小比較を帯分数,整数等の混合の場合へと広げてみようとする姿や
単元が終わるごとに振り返ってまとめをする活動を位置づけた。この活動では,学習内容の再構成をし,学んだことを結びつけ,関連づけて考えることで理解を確かにしていこうとするものである。右の子どもの「算数“きいて!!”」に見られるように,分数の大小比較を帯分数,整数等の混合の場合へと広げてみようとする姿や = = などの相当関係への気づき,さらには,異分母分数の比較へと興味・関心が向く発展的な考えをする子どもの姿が見られた。 などの相当関係への気づき,さらには,異分母分数の比較へと興味・関心が向く発展的な考えをする子どもの姿が見られた。
|







