| 数学トピックQ&A |
|
| アルキメデスの墓標 | |
| Q | 球の体積や表面積の公式は小学校で習ったような気がするのですが,この公式を証明するのは大変なのですね。 「球の体積を求められるか」ということは非常に興味あることですから,人類は相当古い時代に球の体積の公式を発見したのでしょう。 |
||||
| A | 球の体積にちなんで有名なアルキメデスの話をしましょう。 アルキメデス(Archimedes B.C.287〜212)は,紀元前250年ごろ,地中海のシチリア島にいたギリシャの数学者で,「てこの原理」,や浮力に関する「アルキメデスの原理」などの発見者として知られています。彼は,様々な図形の面積や体積について優れた研究をしています。 たとえば,円周率πについては,円に内接,外接する正96角形の周の長さを計算して, 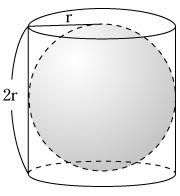 球の体積と表面積について,アルキメデスは,右図のように半径 r の球とそれに外接する直円柱を考え, 球の体積と表面積について,アルキメデスは,右図のように半径 r の球とそれに外接する直円柱を考え,
ここでは,球の体積をアルキメデスがどのようにして求めたかを見てみましょう。 球の体積を求めるには,半球の体積がわかればよい。半球を,図(イ)のように,底面に並行な平面で等しい間隔に切り,図(ア),図(ウ)のように,切り口の円を底面とする円柱と考えると,半球の体積はこれらの円柱の体積の和で近似できる。
図より,「(ア)の円柱の体積の和」<「(イ)の半球の体積」<「(ウ)の円柱の体積の和」が成り立つことがわかる。上の図では半径OAを4等分した場合を考えているが,等分する数をしだいに大きくして,分割をどんどん細かくしていくと,図(ア)の円柱の体積の和は大きくなり,図(ウ)の円柱の体積の和は小さくなり,どちらも半球の体積に近づいていく。 |


