●問題●
次の□に異なる自然数をあてはめて下さい.
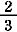 = =  + + 
|
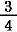 = =  + + 
|
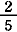 = =  + + 
|
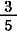 = =  + + 
|
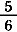 = =  + + 
|
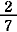 = =  + + 
|
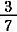 = =  + +  + + 
|
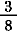 = =  + + 
|
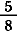 = =  + + 
|
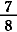 = =  + +  + + 
|
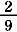 = =  + + 
|
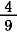 = =  + + 
|
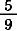 = =  + + 
|
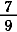 = =  + +  + + 
|
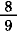 = =  + +  + + 
|
●エジプトの記数法●
古代エジプトでは365という整数を表すとき,
100を表す文字を3個,10を表す文字を6個,1を表す文字を5個
並べた.文字は,こんにちヒエログリフと呼ばれる絵文字である.
現代の我々であれば,11235813(今話題の小説「ダ・ヴィンチコード」に現れる「フィボナッチ数列」)のようにたった10個の数字0〜9でどんな大きな数でも表すことができる.
古代エジプトの数学は我々が想像するよりも水準の高いものであったが記数法(数の表し方)はこのように手数のかかるものであった.
一方,古代エジプトの分数は整数と逆数を表す文字の組み合わせで
 , , 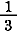 , ,  , , 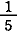 ,… ,…
を表すものであった.
これらの分数  を単位分数という. を単位分数という.
唯一の例外が 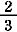 で,単位分数と で,単位分数と 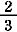 以外に分数を表す方法はなかった. 以外に分数を表す方法はなかった.
現代の英語では 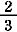 は two third, は two third, 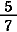 は five seventh と読むが,これらは「 は five seventh と読むが,これらは「 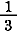 という単位分数 (third) が2つ」,「 という単位分数 (third) が2つ」,「 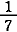 という単位分数 (seventh) が5 つ」という意味で,ここでも単位分数が使われている. という単位分数 (seventh) が5 つ」という意味で,ここでも単位分数が使われている.
さて,古代エジプト人は一般の分数をどう表したかというと,これがまた変わっていて,
一般の分数は,異なる単位分数の和として表す
というものであった.
現代英語のような表現も避けたのである.
これはなぜかと言われても答えようがない.彼らの数学観(あるいは世界観)に基づくものかも知れない.とにかくそれが事実なのである.
●リンド・パピルス●
古代エジプト人が分数などをよく知っていたことは,主にリンド・パピルス(アーメス・パピルスともいう)からわかっている.これは非常に大きなパピルス文書(縦約30センチ,横約5メートル半)で,紀元前1650年ごろ,それ以前の文書からアーメスという筆記者が書き写したものだ.この写本はテーベで見つかり,1858年にスコットランドの骨董収集家ヘンリー・リンドに購入されて,現在は大英博物館にある(参考文献).
リンド・パピルスには分数  ( n は3から101までの奇数)がどのような単位分数の和として表されるかが書いてある. ( n は3から101までの奇数)がどのような単位分数の和として表されるかが書いてある.
冒頭の問題はこのパピルス文書に注目してもらうために出題したものである.
これは一種の実験考古学である.
話題1 初代ローマ皇帝の遺言状
古代エジプト人の分数の表現は,エジプト,ギリシャ,ローマ時代を通して使われていた.
話題2 単位分数分解
どんな分数 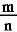 も も
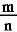 = =  + +  +…+ +…+  + +  (□は異なる自然数) (□は異なる自然数)
と表される.
話題3 埋もれてしまった数学
現代の数学ではエジプト人の分数は顧みられることはない.
話題4 パズルとしての単位分数分解
|