４年	かけ算だったら広さになる？         〜４年「面積」の学習を通して〜
	広島県三原市立田野浦小学校 河野　正史

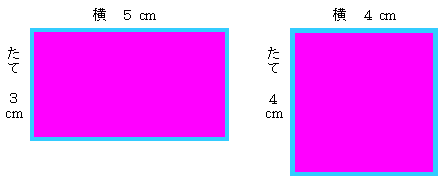
１．はじめに 　長さは「ものさし」で，かさは「ます」で，重さは「はかり」で，それぞれ道具を使って直接的にはかることができる。では広さはというと，直接はかる道具もなく「普遍単位がいくつ分あるか」という量と測定の概念が必要となってくる。 　４年生の面積の学習では初めから公式を覚えたり計算をして量の大きさを出すのではなく，長方形と正方形の「広さ比べ」をする問題から始まっている。子どもたちは２つの図形の「広さ比べ」をしたとき安易に計算をして比べ，「普遍単位がいくつ分あるか」という量と測定の基本概念が忘れられていることはないだろうか。 　この学習の指導過程では，子どもたちが興味を持つような算数的活動の場面を設定し，普遍単位として１辺１cmの正方形の面積「１cm2」を考えることのよさに気づかせ「量と測定の基本概念」の理解を深めたいと試みた。 ２．授業の実際   (1) 　問題の提示 Ｔ 　「今日は広さくらべの勉強をします。四角形のたてと横の長さが（たて３cm　横５cmの長方形）と（１辺が４cmの正方形）はどちらが広いでしょう。」 　子どもたちに考えさせてみると，次のような「たし算」と「かけ算」で比べる２通りの考えが出された。   ●たし算（３＋５＝８　４＋４＝８）で比べた    １０人   ●かけ算（３×５＝１５ ４×４＝１６）で比べた    ２４人 Ｔ 　計算ですぐに出しているみたいだけど，たし算をすると，３＋５＝８は何なの。　４＋４＝８は何なの」 Ｃ 　「たてと横の長さ」 Ｔ 　「うん，たてと横の長さであって，広さかな」 ＊ （１�bのひもを用意していろいろな形の長方形をつくり視覚的に気づかせていった） Ｔ 　「たし算だったら（たてと横）の長さで広さではなかったけど，かけ算なら何がでるの，かけ算だったら広さになるの？」 Ｃ 　「かけ算はなにの計算をしているのかよくわからないので，小さな正方形をいれて数えたらいい」 　平面の大きさをイメ−ジさせるために「面積」でなく「広さ」という言葉で導入を図った。子どもたちは「広さを比べる」ということを意識しながら学習を進めた。しかしながら，安易に計算によって比べようとしている。それもただ計算しただけでその意味については考えていない。 　日常の授業での算数的活動のあり方を見直しながら，「量と測定」の基本概念をしっかり意識させる必要がある。   (2) 　課題の設定 　小さな正方形の大きさはどのくらいの大きさにしたらよいか考えていった。 子どもたちは下のように予想していった。 Ｔ 　「小さなといってるけど，どのくらいの大きさにして数えるの」      ＊子どもの予想    ＊子どもの考え ２�o ６人 （細かくして正確に調べたい） ５�o ７人 （１cmは大きいと思う。） １cm ９人 （１だからよさそう） ２cm 10人 （大きくて線を引くのが簡単そう） 　１cm以外の大きさは，任意単位にした正方形の数が多すぎたりはんぱが出来たりする問題点がある。この問題点が，１辺１cmのよさをクロ−ズアップさせる鍵となるので，任意単位の１辺がそれぞれ２�o・５�o・２cmの正方形とし予想を大切にしていった。また，早くできた子には他の大きさの任意単位を使った考え方にも挑戦させていった。   (3) 　課題の追求 　作図を通して，子どもたちは次のような感想や気づきを持ち子ども自らの力で課題解決できるように学習を進めていった。      ２�o    たくさんかいて難しかった。　すき間ができた。 ５�o やりがいがあると思った。　１cmの方がみやす（やさし）かった。 たくさんかいてむつかしかった。　１cmは大きいと思った。 １cm 線が引きやすかった。　数えやすかった。 余りがでなかった書きやすかった。 ４×４＝１６　　３×５＝１５ ２cm 大きさが違って細長いのができて残った。 　任意単位が大きいとはんぱが出来る，小さいと書くのがたいへん（うまくはまらないこともある）ということを作図を通して体得させながら，１辺が１cmの正方形のよさに気づかせていった。   (4) 　統合化 　１辺が１cmの正方形を単位とすることのよさを感じとらせるために，子どもの気づき・感想を大切にしながら次のようにまとめていった。 ＊小さないろいろな大きさの正方形を敷き詰めて比べてみると   ・ 大きかったらはんぱができやすい。小さくてもはんぱができるし，また書くのが大変だった。   ・ はんぱができない正方形だったら比べることができる。   ・ ２�oや５�oの正方形と１cmの正方形を比べると１cmの正方形が便利だった。   ・ １cmの正方形だと書くのが簡単で早い。大きくてわかりやすい。   ・ １cmの正方形だと数えるとき，３cm→３こ，４cm→４こ，５cm→５こというように数えやすい ＊数えなくても   ・ □cm2が，たての個数×よこの個数＝ぜんぶの個数   ・ たてに□が３こ×よこに□が５こ＝ぜんぶで□が１５こ   ・ （cm×cm）でなく，□cm2が（　こ×　こ）である 　こうした指導過程を通して，子どもたちは普遍単位「１cm2」のよさ，それと普遍単位のいくつ分という「量と測定」の基本概念についての理解を深めていくことができた。 ３．実践を終えて   ○ 　面積を考える際、１辺１cmの正方形を単位とすることのよさは，長さ（cm）を表す数とたてまたは横にならぶ正方形の個数（こ）を表す数が一致することである。個数であるから公式（たて×よこ）と簡単に計算できるよさについて理解することができた。   ○ 　子どもの中から，「あ−そういうことなんか」「そうなんか」「ああーようわかった，ようわかった。」という声も聞かれた。   ○ 　問題提示の場面で，（たて＋よこ）で比べた子が多くいた。生活経験を優先して考えたからだと思われるが，「周りの長さで比べる」という考えは誤りであるが，成り立つ場合もある。もっと教具等を工夫して子ども自らがその考え方が誤りであることに気づかせていく必要もあった。   ○ 　算数的活動を設定し，普遍単位の正方形の大きさが「１cm2」のよさ・便利さを気づかせる指導過程をしくんでいった。それは子どもの脳裏に「量の測定」の基本概念をしっかり焼き付かせておきたかったからである。子ども自らが意欲的に取り組み追求し続けられるような指導過程はどうあるべきか，今後も研究を進めていきたい。