順列と組み合わせ
一般に,互いに異なるn個のものからr個取り出して,それを1列に並べるとき,その並べ方を,n個のものからr個取る順列といいます。
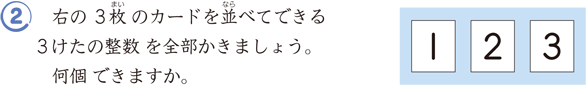
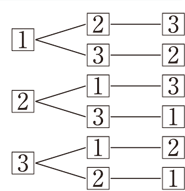
上の例は,3つの違った数1,2,3の順列をつくる問題ですが,これを右のような図に,順序よくかいていくと,すべての場合を落ちなく重なりなくあげることができ,順列の数6も求められます。このような図を樹形図といいます。
組み合わせは,1つの集合の中からいくつかの要素を取り出して組み合わせる仕方です。順列と似ている点は,起こりうるすべての場合の数を求めるという点で,異なる点は,並べる順序は問題にしない点です。例えば,順列では,(A,B)と(B,A)は違うものになりますが,組み合わせでは同じものを表していることになります。

数学的には,4個のものから3個取り出して並べる順列の数は,4P3=4×3×2=24となります。
また,4個のものから3個取る組み合わせの数は,
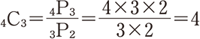
となります。
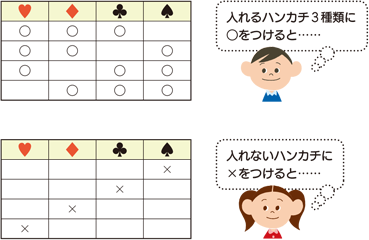
また,4C3=4C1ですから,上の問題では,どのハンカチを残すかを考えても解決することができます。
なお,第6学年の学習としては,表にかいて調べていくとよいでしょう。