直線の垂直・平行の関係

平面における直線の垂直・平行は，２本の直線の位置関係を表しています。位置関係ですので，２ 本の直線の長さには，全く関係ありません。位置関係を成立させる条件だけを保っていれば，それで十分です。
その条件として示されてくるのが，垂直の場合であれば，「２つの直線が直角に交わる」ということです。この条件を満たしさえすれば，２つの直線は常に垂直の位置関係になるわけです。

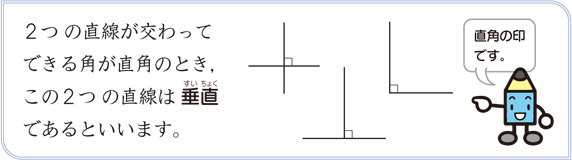
もちろん，２つの直線が実際には交わっていなくても，伸ばしていったときに直角に交われば，この２つの直線はやはり垂直になるわけです。
一方，平行は，はじめは「どこまでいっても交わらない２つの直線」として受け止められがちです。平行のイメージからすれば，確かに「どこまでいっても交わらない２つの直線」ですが，しかし，この表現では，「どこまでいっても交わらない」という保証を，実証的にも理論的にも得ることができません。
ですから，観点を変えて，垂直の概念を用いて，次のように概念規定を図っていくことになります。

単元名を「平行・垂直……」としないで，「垂直・平行……」というように，垂直を先に取り上げているのも，垂直でもって平行の概念を規定しようという事情があるからです。