
 |
“数学と生活との結びつき”を実感させる数学授業の創造
高知県立安芸桜ケ丘高等学校
島田 佳幸
1.はじめに
残念なことだが,「数学嫌い」が増えてきている。本年度入学生も同様で,「中学校の時,数学は好きでしたか?」という問いに7割強の生徒が(どちらかというと)好きではないと答えている。しかし,「数学は社会に必要ですか?」という問いに対しては,8割の生徒が(どちらかというと)必要と答えている。必要だが好きではないというのは,生徒の中に,数学がより身近な存在となっていない表れだと考える。数学と現実の距離が縮まっていないのである。
また,学力面ではどうかというと,4月のはじめのテストの結果,「3−7」が解けない生徒が2割弱,「−2−(−7)」は2割強,「−3 2 ×(−2)」に関しては7割が不正解だった。九九が不完全な生徒の数も増えてきている。
学習を成立させるためには,生徒の心の奥底に眠っている「学びたい」「わかりたい」という人間本来の要求を引き出させる必要がある。そのためには,学習は生徒の知的好奇心を呼び起こすものであって,しかも自分の力でそれをやり遂げたという実感が持てるような教材開発が教師に求められる。様々な学力の生徒がいても,どの子も同じスタートに立って学習できる高校生にふさわしい教材を与えていけば,過去の学力差にこだわることなく,みんなが授業に参加できるようになると考える。
以上のような状況を踏まえ,本研究は,生徒一人ひとりに数学の楽しさを体感させ,高校生としての学力の回復を目指すものである。
2.授業実践の経過
数学Iの第1章「数と式」の単元の4分の3は中学校の内容が占めている。4月当初から学力差が目立ちやすく,「できる」「できない」がはっきりしている単元である。それゆえ,生徒の劣等感を助長しやすい単元になる危険性を秘めていると言える。そこで今年は数学Iの最終章「三角比と図形」から始めることにした。この単元は中学数学では扱わず,学習者のすべてがはじめて学ぶのであり,同じスタートラインの立てるという利点がある。
主題を実現するために,2つのポイントを設ける。1つは,“4月当初の授業展開の重要性について”,もう1つは,“地域と数学のつながりが見える授業の創造”である。
[ポイント1] 4月当初の授業展開の重要性
授業進行のテーマを「物の高さをどうやって測ればいいのか」とし,小中学校で習う“比”を取り入れ,高校数学のタンジェントに結び付けていった。ここで重視したのが実験実習である。“数学と生活との結びつき”を生徒の中に取り戻し,今まで学習したことと,高校数学との距離を縮めるのが目的である。
授業構成は次のとおりである。
 討論によって数学を身近なものにする
討論によって数学を身近なものにする
入学しての最初の授業の様子である。
学習するための導入として,実生活の中でありそうで実感しやすい出来事を想定して問いかけを行う。その最大の利点は“興味づけ”にある。架空とはいえ,生活の場面を提示することによって,数学と現実の距離を縮めるのが目的である。生徒の顕著な数学へのコンプレックスを払拭する利点が大きい。
 実生活の場面へ「問題」を投じる(発問)
実生活の場面へ「問題」を投じる(発問)
- 教師Q:
- 1枚の写真を黒板に貼り,生徒に「この写真はグラウンドの海側にあるちょっと有名な木です。この木の高さを測るにはどうすればいいでしょうか。」
- 生徒A:
- 「トランポリンでジャンプして測る」
- 生徒B:
- 「リモコンのヘリコプターを飛ばして測る」
教師は生徒の意見をカテゴリーに分け,すべて黒板に書いていく
↓
 生徒の答えを分析していく過程でより高次解決法に対する「疑問」を生み出す。
生徒の答えを分析していく過程でより高次解決法に対する「疑問」を生み出す。
- Q→A:
- 「木の枝が張り出していて木の天辺までジャンプできない。どうしたらいいのか」
- Q→B:
- 「海風が強くリモコンヘリを操縦できない。どうするか。」
- 教師Q:
- 「もっと労力のかからない測り方はないか?」
↓
 同質場面の数学的“解決”法を探る
同質場面の数学的“解決”法を探る
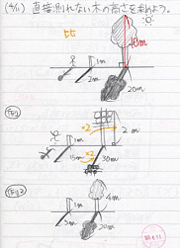
生徒のノート

実験実習風景![]()
(影を使って校舎の高さを測る)
生徒からは本当にユニークな回答が返ってくる。それら一つひとつの意見を尊重しつつ,もっとも労力のかからない方法はないのか?と議論を促し,生徒からの「影を利用する」という方法を採用していく。そして,授業の中で生徒から出てきた意見や考え方をもう一度生徒に投げ返し,討議し,その考え方から,これから学ぼうとする正弦定理,余弦定理の基礎付けを行っていくのである。
また,上記![]() で示される解決は
で示される解決は![]()
![]() を主体的に取りくむことにより効果的なものとなり,驚きと喜びを引き出させる。すぐに結果を示すのではなく疑問を提示し,その糸口から生み出される様々な“考える”という行為を重視し,またその時間も保証していくのである。これらの段階を通ることによって数学の必要性が実感できるのである。
を主体的に取りくむことにより効果的なものとなり,驚きと喜びを引き出させる。すぐに結果を示すのではなく疑問を提示し,その糸口から生み出される様々な“考える”という行為を重視し,またその時間も保証していくのである。これらの段階を通ることによって数学の必要性が実感できるのである。
『高校に入って初めての授業だったので,不安が大きかったけど,わかりやすく教えてくれて安心しました。影を使うのは思いつきませんでした。他の人の意見が聞けて,測り方もいろんな方法がある事が分かりました。数学はあんまり好きじゃないけどちょっと好きになりそうな感じ。これから難しくなると思うけど頑張りたいです。』これは,第1回目の数学の授業の感想である。高校入学時の生徒は,これからの高校生活を思い希望や不安でいっぱいである。しかし,授業に対する“やる気”は高校生活の中で一番高い。この時期は,嫌いな教科を好きにする絶好の機会なのである。教師が一つひとつ丁寧に生徒に向かい合い,一工夫加えた教材を提示することによって,生徒の数学に対するコンプレックスが払拭されていくのである。
授業の最後には,生徒に今日の授業の感想や進むスピードの具合,生徒自身の授業の取り組み方,質問等を「一言メッセージ」としてノートの最後に書かすようにしている。この「一言メッセージ」を読み次回の授業にフィードバックさせていく。
 実験実習を行って生徒の意見を実証する
実験実習を行って生徒の意見を実証する
影を使って物の高さが測れるということを証明するために実験実習に取り組んだ。授業の興奮が冷めないうちにすぐ行動に移すということが重要になってくる。
まず教室で,3人一班の班を作り,1m棒とメジャーと授業プリントを渡す。そして,この実験実習の統一テーマを校舎の高さを影を使って測ることとし,各班ごとにもう1つ好きなものの高さを測るという2本だてにすることを説明する。その後,生徒は班ごとに測量を開始する。
授業プリント![]()

実験実習風景![]()
(影を使って木の高さを測る)
『今日の授業は,影を使って物の高さを調べる実習をしました。正直はじめは「そんなことができるわけないやんか」と思っていたけど,実際に測れて,校舎の本当の高さとの誤差も10cmというのにも驚きました。今まで数学で外に行って実験したことなどなかったので良かったかなと思います。しかし弱点の,太陽が雲に隠れてしまって調べれなくなって,待つのがちょっと面倒くさかったです。またやりたいです。』
今回の実験実習を通しての生徒の感想である。
この時点で自分が学んでいることが,机上だけでなく現実のものだと認識していくのである。また数学嫌いの生徒が,次回の授業は何をするの?と数学の授業に興味を持ち出す。
影を使って校舎を測定した結果,14.2m〜19.5mの幅で測定値が出てきた。そして平均を取ると18.3mという値になった。実際の校舎の高さは,18.2mであり,生徒たちは,影を使うという原始的な方法でもだいたいの高さは分かると言うことを認識するのである。
 授業の流れにそって定義を使う
授業の流れにそって定義を使う
授業進行を「物の高さをどうやって測ればいいのか」という一連のテーマのもと,タンジェントの定義も変化させた。教科書ではタンジェントを比の割合(底辺分の高さ)で定義しているが,今回は直角三角形の底辺が1の時の“高さ”がタンジェントというように,長さ(量)で定義した。このほうが実際のものの高さを求めるのに適している。
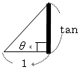 生徒は前回の実験実習で,影で物の高さを測れることを学んだ。しかし最大の弱点が,太陽が雲に隠れてしまって影が出ない事というのを認識する。その代償が雲から太陽が出るのを“待つ”という時間だった。高校生は,すぐに結果を欲しがり極端に“待つ”ことを嫌がる。そこで,弱点を克服するアイテムとしてタンジェントを導入した。生徒からは,「本当にこの方法で弱点はないの?」と半信半疑だったが,生徒は一様に興味を示した。
生徒は前回の実験実習で,影で物の高さを測れることを学んだ。しかし最大の弱点が,太陽が雲に隠れてしまって影が出ない事というのを認識する。その代償が雲から太陽が出るのを“待つ”という時間だった。高校生は,すぐに結果を欲しがり極端に“待つ”ことを嫌がる。そこで,弱点を克服するアイテムとしてタンジェントを導入した。生徒からは,「本当にこの方法で弱点はないの?」と半信半疑だったが,生徒は一様に興味を示した。
その後タンジェントを使い,木の高さやビルの高さを求める演習をこなしていく。
『英語の筆記体を数学で習うとは思っても見なかった。最初は難しそうだったけれど,問題を解いているうちに,案外簡単だと言うことが分かった。全部できてた。数学が面白くなってきた。先生ありがとう。』生徒の声である。
 前回の弱点克服のための高次解決法
前回の弱点克服のための高次解決法

測角器
実験実習第2段として,「5円玉で学校を測ろうプロジェクト」に取り組んだ。このプロジェクトの目的は,身近で身の回りにある道具だけを使い,物の高さを実測するという体験学習を通して,大まかな値を楽しむことにある。
まずは角度を測るための“測角器”を作成する。前日に5円玉を持ってくるように支持をしておく。授業では生徒に何の説明もせずおもむろに,ストローやMOケース,厚紙,分度器,糸を配る。何が始まるのか生徒の目が輝いている。そして5円玉を机の上に出させ,ここで初めて測角器の説明をする。この時点では全ての生徒の関心は授業に向いているのである。

側角器作成の様子
分度器を厚紙に張り,5円玉に糸をつけて固定し,MOケースに貼り付けると出来上がりである。のぞき穴のストローを取り付けるのがポイントである。 『ストローが配られた時は何が始まるのかと思っていました。説明を聞いているうちに全貌が分かったけど,本当にそんなんで角度が測れるのと疑問でいっぱいでした。けれど黒板の上の時計との角度が測れてビックリしました。自分で作る授業は面白いです。』生徒の感想である。

目の高さ測定風景
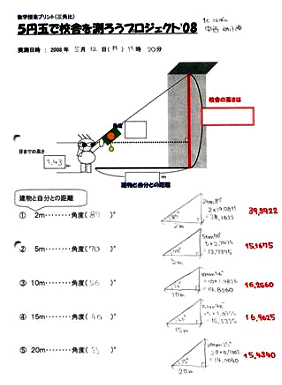
次に3人一組でお互いの目の高さを測った。以上で準備完了である。そして実測するため外に行くのだが,立ち位置によって“測りづらさ”を体感してもらうために,校舎から測定者の立ち位置の距離を2m,5m,10m,15m,20mと5箇所に設定した。
測定結果は表1のとおりである。そしてクラス全体の平均を取ると17.8mという値になった。
このプロジェクトを通じての生徒の感想文を見てみる。
| 校舎と測定者との距離 | 校舎の高さの平均値 |
|---|---|
| 2m | 17.5m |
| 5m | 16.0m |
| 10m | 15.5m |
| 15m | 16.6m |
| 20m | 18.2m |
『同じ校舎を測るのに5カ所とも違う数字になった。1度単位できちんと角度を見ないと正確には計れない。特に2m地点からの角度はあやしい。真上に向かないといけなかったし,首が疲れた。これらのことが今回の結果になった。次にやるときは息を止めてジッとしたい。しかし,20mから測ったときの答えが校舎の高さとピッタリ合ったのがすごかった。曇っててもできたのが嬉しかった。』
感想の中でも出てきているが,対象物との立ち位置によって“測りづらさ”も実感し,生活の知恵として認識していっている。

測角器による測定風景
授業プリント![]()
単元の最初の興味づけがきちんとできていると,生徒たちは次回の学習内容への興味が増してくる。その状態で体験学習を導入すると,学習内容の印象も強い。学び体験することによって次の授業へとつながっていくのである。学習は教え込まれ,覚えるものではなく“自分の力で学び取ろう”とする姿勢がなければ成立しないものだということも認識していく。
ここまでの授業展開の中で,中学数学から高校数学への橋渡しの基礎ができた。数学に対するあきらめ,苦手意識は生徒から払拭され,授業の感想も前向きなものが多く返ってくるようになった。現実と数学とのつながりが目に見えた時,自ずと数学は生徒にとって身近な存在になってくる。
[ポイント2]地域と数学のつながりが見える授業の創造
さらに,学習の範囲を学校から自分たちの住んでいる町に広げていった。授業のテーマは「地域から数学を考えよう」である。そして生徒自身の手による問題集「ごめんなはり線で数学をしよう」を作り上げた。以下,問題集づくりにあたった過程を具体的に見ていくことにする。
 2つのテーマを調査する
2つのテーマを調査する

コンピュータ実習風景
自分の住んでいる地域の良さを再認識する役割を持たせるために,問題作成の題材を2つ提案した。1つは“自分たちの住んでいる町”,もうひとつは,安芸桜ケ丘高校生の通学の足である“ごめんなはり線”にスポットを当てた。
自分たちの住んでいる町にポイントを置くことは,過疎化の進む高知県で,未来を担う若者が生まれ育った市町村の発展のための一役を担えるようにとの願いをこめてのことだった。 そして問題を作るときの約束として,できるだけ現実味のあるものにすること。そのために,題材になるものをよく調査し,他県の人が見ても興味を持つような問題を作成するように指示した。
生徒は,地域の中で自分の好きな題材を選び,放課後や休みの日を使って携帯電話内臓のカメラで撮影していった。その後,撮影した名物や名所,史跡などの詳細をインターネットで調べ,画像と説明をワンセットにまとめていくという作業を行う。
 生徒が問題をつくる
生徒が問題をつくる

問題集表紙
問題作成に関して,その題材になるものの説明(歴史的背景等)を前半に入れ,その後に数値の入った問題文を入れるよう統一した。ここでは生徒自身のカラーが出るように,手書きの説明図を付け加えるように指示する。
この問題作成という過程は,授業の内容が完全に理解していないと出来ない作業であり,生徒は教科書とノートを何回も見直し,また友人と議論しあい,一つの作品を完成していくのである。
最後にパソコン上で,画像と問題,手書きの説明図,解答の4点のレイアウトを行い,世界に1つだけの問題集「ごめんなはり線で数学をしよう」を完成させた。以下,生徒の感想と作品である。
『問題の写真は,登下校時に通る道で撮った。毎日見るものだから親しむことができてよかった。問題の文章を書く時は,インターネットも利用して情報を集めた。たくさんある情報の中から使えそうな情報を抜き出す作業が今回の学習では,一番面白かった。自分で問題を作るにはちゃんと学習内容が分かっていないとできないのでなかなか良い勉強法だと思った。また,みんなの作った問題を見て,高知にはいろんなところがあるなって発見もできて良かったし,大量のプリントを見るとがんばったなーと思えた。違う問題も作ってみたい。』
生徒の感想文の一部だが,感想をクラスの全員がA4の感想文用紙にビッシリ書いていて,今回の問題作成の授業の生徒の反応の良さに驚いた。また,冊子作成の過程における生徒のいきいきとした表情や,完成したときに作品を熱心に読みふけっている様子を見ると,創造的な学習の楽しさや,同学年の他の生徒の作品を知ることは,数学に対する興味付けという点に大きな力を発揮する。
|
<生徒作品 |
|||||||||
|
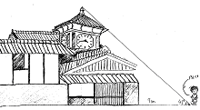
僕らの野良時計を測ろう! |
|||||||||
 |
 |
||||||||
| 野良時計は安芸のシンボル的な建物です。野良時計がなぜ安芸のシンボルになったのか?そこには時計好きな一人の若者の汗と涙の物語がありました。野良時計は今から110年余り昔の明治20年ごろ,この土地の地主だった畠中源馬氏によって作られました。時計に魅せられた源馬氏は,西欧から時計を取り寄せ独学で研究し,そして分銅も歯車もすべて手作りで野良時計を完成させた。この頃時計などなかったので,野良仕事をしていた人達に時間を知らせていました。これが野良時計の所以です。 この野良時計からの問題です。 野良時計から3m離れた地点に観光客のちっちゃいおばちゃんが立っています。おばちゃんの身長は132cmです。おばちゃんの足元から野良時計のてっぺんまでの角度は64°でした。さて,野良時計の高さは何mでしょうか? |
|||||||||
|
|||||||||
|
<生徒作品 |
|||||||||
|
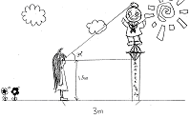
あかのカモメちゃんの高さを求めよう |
|||||||||
 |
 |
||||||||
| ごめん,なはり線の人気のーつは,なんといっても大きく広がる太平洋をながめながら走ることです。最高のロケーションを持っている駅のひとつに赤野駅があります。その駅には太平洋を気持ちよく飛んでいるカモメをモチーフにした あかのカモメちゃん がたっています。 ここで問題です。 あかのカモメちゃん から3m離れたところから1番上を見上げると34°ありました。カモメちゃんの高さを求めなさい。ただし目の高さを1.5mとします。 |
|||||||||
|
|||||||||
 問題集「ごめんなはり線で数学をしよう」の構成
問題集「ごめんなはり線で数学をしよう」の構成

ごめんなはり線各駅のもくじ
最後に,生徒の作った問題を冊子にしていく。その時に,“自分たちの住んでいる町”と“ごめんなはり線”との2つの内容が融合できるように,観光パンフレット的役割を持たせた。ごめんなはり線の各駅の案内版のページから,生徒の住んでいる町の自作問題の名所や史跡等まで導いていくというものである。「この駅から・・・に行ってみよう」といった様に書き加えた。こうすることによって,生徒たちが自分たちの住んでいる地域を知るということもできるし,単元を変えても,どんどん地域を掘り起こし,この問題集「ごめんなはり線で数学をしよう」に付け加えていけるのである。
3.おわりに
これらの授業を終えた後,再度アンケートをとり変化を見てみた。
「高校に入って,数学は好きになりましたか?」という問いにほぼ全員の生徒が(どちらかというと)好きになったと答えている。また,「数学は社会に必要ですか?」という問いに対しても,ほぼ全員が(どちらかというと)必要と答えた。これらのことは生徒の中で,数学がより身近な存在となってきた表れで,“数学と現実の距離が縮まった”と考えられる。
以下,授業を受けた生徒の感想である。
『この授業を取り組んで,自分としてはとても分かりやすかったです。まず、自分たちの手で、測角器を作り,そして,実際に使ってみて面白かったし,勉強にもなりました。また、ケイタイで家のそばの木を撮ったり,ごめんなはり線の駅を撮ったりして,自分たちの生まれ育ったところの良さを,改めて実感することができました。それともう一つ,問題を作る時,問題を解くのは分かっているのに,逆に問題を作る側になってみると,うまく数が合わなかったりして疲れました。
数学というのは,あまり生活とはかかわっていないものだと今まで思っていたけれど,今回のプロジェクトを通して,自分の生活の中にかかわっているのだなーと再発見しました。こんな楽しい授業だったら、またやりたいです。』
生徒たちは,“自分の住んでいる町”を自分の足で調査し,再認識していく過程で人と人とのつながりのすばらしさを実感した。そして,それを授業に還元し問題集作りという形にしていく。更に,自分以外の人にも自分の作成した問題を見てもらいたいとアピールするようになる。ただ「問題が解けたらいい」というだけの授業への参加形態から,数学の本質を追求してくことの面白さを体験していくといった授業の主人公としての本来あるべき姿へと変化していった。
また,次のような感想文もある。
『・・・問題文を作る時少し困った事があった。今まで考えてなかったけど,ヤシの木の高さが分からなかった。インターネットで探しても見あたらないし,どうしょうと思って取った最後の手段が,自分がヤシの木の横に立った写真を撮り,自分がヤシの木の何等分になるかで何とか乗り切った。・・・』
今までの知識を応用して困難な局面を乗り切っている様子が伺える。これこそが学びを基礎にした「生きる力」が生徒の中で芽生えた瞬間だと考える。
これらの実践を通じて得られた手ごたえを核心に変えるために,これからも更に授業実践を重ねていきたい。
|
|||