
 |
児童の思考のつながりに着目した文章問題(数量関係)への取り組み
大阪府東大阪市立枚岡東小学校
神保 勇児
1.主題の意味するもの
学習指導要領(D 数量関係 (1)「D数量関係」の領域のねらい)から,「…(中略)… 今回の改訂では,言葉,数,式,図,表,グラフなどを用いた思考力,判断力,表現力等を重視するため,低学年から「D数量関係」の領域を設け,各学年において充実を図っている。この領域では「関数の考え」,「式の表現と読み」及び「資料の整理と読み」が主な内容となっている。(中略)… 」また,学習指導要領解説 第3学年(D 数量関係)によると「D(1) 除法の式 …(中略)…指導に当たっては,これまでの加法,減法及び乗法と同様に,数量の関係を式に表したり,式を読み取ったりすることを重視することが大切である。式に表す指導に際しては,…(中略)… 言葉(文章)による表現,○やテープなどの図を用いた表現,具体物を用いた操作などと関連付けながら,式の意味の理解を深めるとともに,…(中略)… 第3学年では,式の指導において,具体的な場面に対応させながら,数量や数量の関係を式に表すことができるようにするとともに,式が表している場面などの意味を読み取ったり,式を用いて自分の考えを説明したり,式で処理したり考えを進めたりするなど,式を使いこなすことができるようにする。図の指導においても,数量や数量の関係を図を用いて表すこと,図に表された数量の関係を読み取ること,図を用いて自分の考えを説明することなどができるようにする。さらに,式が表していることと図が表していることが同じであることなどについて理解できるようにする。…(中略)… 第3学年では,未知の数量を□などの記号を用いて表現することにより,文脈通りに数量の関係を立式し,□に当てはまる数を調べることができるようにする。…(中略)… 未知の数量を表す記号として用いる場合を中心に指導し,□などの記号を用いて立式したり,図に表すことと関連付けたりして,数量の関係を的確にとらえることができるようにする。…(中略)… 」
このことから,数量関係を考える上で言葉や図,式であらわしていくことが重要な活動となってくる。さらに,児童の思考を交流させ学習を深めていくことが今後の算数指導に必要なことである。
2.主題達成に向けて
予め授業実践の前にアンケートを行った。その結果は,児童の約90%が「算数を好きと答えている」,児童の約96%が「授業で友達の考えや意見が役に立つと答えている」であった。しかし,児童の67%が「問題を解くときの計画(見通し)を立てられていない」,児童の77%が「授業の終わったときに「今日はがんばった」という気持ちになると答えている」という結果も得られた。
この結果から,学級の児童は算数が好きで友達の考えや意見が役に立つと考えているが,問題を解くときの計画(見通し)が立っておらず,授業の達成感をあまり感じていないのではないかと考えた。そこで,今までの学習を生かして見通しを持ちながら取り組めるよう,発展的な倍数関係を考える課題を設定した。新たな課題に試行錯誤しながら取り組み達成感を得られるようにしたい。また,自分の言葉で表現すること,関係図等を使い数量関係を考えること,式で表すことに取り組ませたい。
3.具体的な手立て
(1)予習
学習においてあらかじめ見通しを持ち課題に取り組むことは課題解決の観点から非常に重要である。特に学習開始時にレディネスが形成されていれば,どの子も学習に取り組みやすくなる。また,ただ予習するだけではなく,観点を絞った予習をすることで課題がより明確化する。予習を授業で活かすことで,学習の深まりがさらに期待できると考えられる。具体的には予習は予習プリントを使って行う。これは,予習の仕方を勉強していくための手立ての一環である。予習プリントには次の項目を挙げた。
- 単元名
- 今日勉強したことを1行でまとめて書きましょう。
- 問題(問題はあらかじめ伝えておく。)
- ぱっとえだやふきだしが書けるように,先に作るざいりょうを作っておきましょう。
もちろん,図やけいさんもかいていいよ。 - 明日勉強するときの目ひょうを1行で書きましょう。
これまでの児童の変化
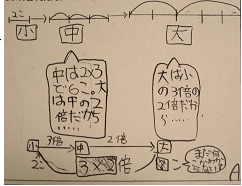
(写真2)

(写真1)
写真1「たし算とひき算」(平成20年9月),写真2「ドルフィンのまほう学校 何倍になるのかな」(平成20年10月)のある児童Aの予習である。最初,言葉だけの表現によるものだったが,指導をしていくうちに図や言葉や式を使いながら表現できるようになった。
(2)ノート指導
児童はこれまで自分と自分,自分と友達の思考のつながりを意識し,言葉や図を用いながら思考過程をノートに記述する取り組みをしてきた。児童が算数を学習していく上で,どのように理解を深められるかがとても大切なことになってくる。課題を解決する上で児童の作りだした数学的なアイデアにつながりが生まれたときに初めて学習の理解が深まると考えられる。そこで,次のことに注意して指導してきた。
- この考え方と似た考え方はないか。
- 似ていないとき,どこがにていないのか。
- 今の考えとつながりそうなところはあるか,ないか。
写真3「あまりのあるわり算」(平成20年9月)のある児童Bのノートである。言葉や図,式で,自分の考えたことを自在に表現している様子が分かる。

(写真3)
(3)授業
授業では児童の発表や質問等を中心におき,式や言葉,図の観点から学習を行ってきた。 ノート指導と合わせて思考のつながりをより具体的にするために,以下のことに気をつけて指導している。
・発表について
- 発表者
-
- 発表した考えは,聞き手が納得できたものかどうか確認する。
- 発表者が言葉だけでは説明させず,発表者自身が板書している図・式等を動作を入れ,指し示たり,書きながら説明できるようにする。
- 発表者が考えたところまでを述べ,他の児童に付け足しをさせる。その際,思考過程がつながっていることを意識させる。
- 聞き手
-
- 発表者の表情を見るようさせる。
- 反応をさせる。(挙手による納得できたかどうかの確認,発表者が発した言葉への質問)
- 必要なことがあればメモをさせる。
・話し合いについて
- 自分で考えわからなければ友達と相談する。
- 相談して分かったことはノートに記述していく。
(4)振り返り
振り返りを書くことはその日の授業の自分を見つめ直し,反省し明日への課題を見つけることで復習にもつながり非常に有用な手段である。今回の実践では振り返りを算数日記という名前で行っている。これまで児童は,今日学習したこと,友達のいいところ等を観点として取り組んできた。振り返りでは,言葉のみの表現も大切だが,式や図を加えた多様な表現ができれば,より学習が深まると考えている。
4.授業実践
(1)目標 変量に着目し,何倍になるかを考えて問題を解くことができる。
- (関心・意欲・態度)変量に着目した考えを使って,日常の問題を解決しようとする。
- (数学的な考え方)変量に着目し,何倍になるかを考えることができる。
- (表現・処理)変量に着目し,何倍になるかを考えて問題を解くことができる。
- (知識・理解)a倍のb倍が(a×b)倍になることを理解できる。
(2)系統
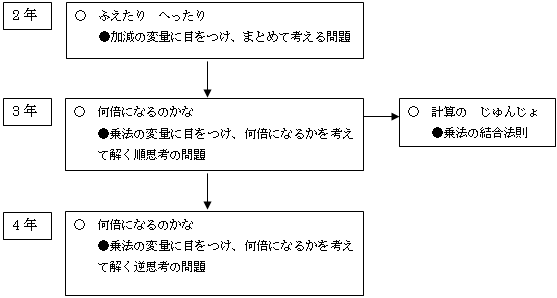
(3)学習指導計画(総時間数3時間)
| 目標 | 学習活動 | おもな評価基準 |
|---|---|---|
第1時
|
|
|
第2時
|
|
|
|
||
第3時(本時)
|
|
|
(4)本時案
本時の目標
- 文脈から倍数関係に気づき,問題を解決することができる。
- 図や式,言葉を使い,問題解決を工夫することができる。
| 学習内容 | 指導・留意点 | 評価 |
|---|---|---|
| 問題提示学習内容の把握 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 問題
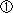 青,赤,白の3種類のはこがあります。
青,赤,白の3種類のはこがあります。
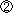 赤のはこには白の4倍,
赤のはこには白の4倍,
 青には赤の2倍はいります。
青には赤の2倍はいります。
 一番たくさん入るのはどの色のはこですか。
一番たくさん入るのはどの色のはこですか。
(5)授業の実際と考察

(写真4)
全体の学び合いでは写真4のようにそれぞれの児童が考えた図や式や言葉をホワイトボードに書きながら説明している。書きながら説明することで,聞き手の児童の視線は発表者の児童の言葉と手の動きに集まる。発表の仕方を見れば,どの順番で考えていったのがかがよく分かるため,他の児童は聞きながら理解を深めることができる。また,聞き手の児童はその発表を書き加えることで,更なる学習効果が生まれる。それが,児童Cのノート(写真5)である。友達の発表した内容をノートに書き,さらにふきだしを加えている。
(写真5)
- 児童Cのふきだし
上の内容について -
- 白の数がわかってその順番でしたらわかる。
- わかりやすい
- 下の内容について
-
- わかりやすい
- ○○と似ている
- どこに気を付けているか。
実践では,友達の考えに自分の考えたことや思ったことを加えていく児童の姿が見られた。また,ノートに加えていく過程で疑問に思ったことや,発表者の気をつけたところ,工夫したところを質問しようとする様子も見られた。
・文字を使った考え方

(写真6)
教科書の問題では一番小さな箱に入る数が分かっていたが,本時ではその数が分からない。ここでは白の箱に入る数が分からないので,児童Dは白の箱に入る数を「?」として考えた。 未知の数量を「?」などの記号を用いて表現することで,文脈通りに数量の関係を立式することができ,「?」に当てはまる数を調べることができる。自力解決の際,児童Dは「白の数がもし分かったら,その数を?に入れれば答えがわかる。」と言っていた。そして,その考えを自分の言葉を使って友達にわかりやすく説明することができた。(写真6)
- C:
- 最初に,白の数が分からないので「?」にしました。その「?」に4をかけたら赤の箱に入る数が分かります。それで,次に赤の数を「?」にして,青は赤の2倍だから2をかけると,青の数が分かります。だから,一番多いのは青の箱です。
- T:
- 今の発表で納得できた人はいますか。
- T:
- では,どんなところが納得できましたか。
- C1:
- ○○ さんの数を「?」にして計算していたところが分かりやすくて納得できました。
- T:
- では,質問がある人はいますか。
- C2:
- なぜ,「?」を使ったのですか。
- C:
- 白の箱の数が分からなかったからです。
- C3:
- 赤の「?」は何ですか。
- C:
- もとの白の数が分からなくて,その4倍だから赤の数もわからないので「?」にしました。
未知の数量を表す記号として「?」を用い,言葉や記号を用いて立式することができ,数量の関係を的確にとらえることができた。
・具体的に数を決めた考え方

(写真7)
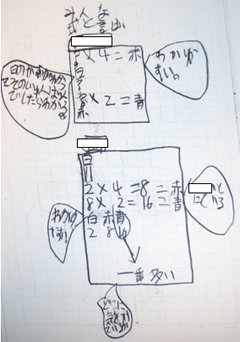
数の大小の根拠となる数がないので,問題で倍数関係の基準となる白の数を児童自身で決定していた。具体的な2や4など比較的計算しやすい数を選択し,赤・白・青の関係を明らかにする姿が見られた。写真7では式を中心にして,言葉で補いながらわかりやすく記述している。この他にも文章のみで説明しているものもあり,児童の共感を得られるような考え方を示すことができた。
- C:
- まず,白の数を2と自分で決めました。次に赤は4倍なので4をかけて,赤の数が8と分かりました。そして,青は赤の2倍なので,8を2倍して青の数が16になりました。最後に白は2,赤は8,青は16なので一番多いのが青だということがわかりました。
- T:
- 今の説明で納得ができた人はいますか。
- T:
- では,質問がある人はいますか。
- C4:
- どんなところに気を付けてしましたか。
- C:
- 計算を間違えないようにと何倍になるのかを気を付けてしました。
- C5:
- どんなところに工夫しましたか。
- C:
- 白の数が分からなかったから,自分で2と決めたところが工夫したところです。
具体的な数値を使って,倍数関係を利用して数の大小関係を明らかにすることで,わかりやすく説明することができた。
・関係図をもとにした考え方

(写真8)
教科書で学習した関係図を用いて倍数関係を明らかにすることもできる。本時までに学習した関係図は大小関係で一番小さいものの数が明らかになっていたが,本時では問題に提示されていない。そこで,児童の工夫が見られた。写真8では白,赤,青にそれぞれの倍数関係を書き込み,関係図からわかることをまとめている。このことにより,具体的な数値を決めなくても,倍数関係のみでそれぞれの大小関係を知ることができる。
本時では,大小関係の把握のために,倍数関係のみで大小関係を決定する考え方は高度な考え方だと位置づけ説明をするにとどめ,具体的な数値を使う考え方と記号を使って考える方法を推奨し学習を進めた。そこで,まとめを「数字をあてはめる」「?などの記号を使って考える」として,本時の学習を終えた。本時の板書は写真9の通りである。

(写真9)
(本時の学習後の算数日記)
(写真10)

(写真11)
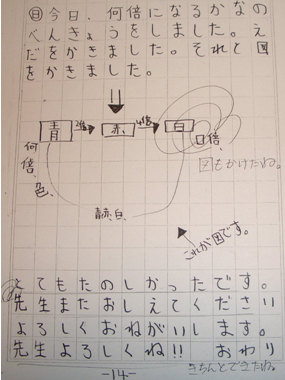
学習後の児童の振り返りを読むと,自分の学習を振り返り図を描いている児童(写真10)や文章で自分の学習を振り返る児童(写真11)から,倍数関係において図を使うこと,数字の当てはめることや記号を使って考えることの重要性に気づき,理解することができたと考えられる。
5.成果と今後の課題
(1)成果
児童は,文脈から倍数関係に気づき,問題を解決すること,図や式,言葉を使い,問題解決を工夫することができた。特に,「言葉と式」,「図」と観点別にして,倍数関係を明らかにするために創意工夫をすることができた。これは,新学習指導要領の改訂の重要な視点として示されている「言語力の育成・活用の重視」にも関わってくる。言語力には,書く力・聴く力・話す力・伝える力などがあるが,本実践における予習・ノート指導・発表や質問・振り返りから本実践で十分な成果が得られたといえる。また,予習段階で同じ問題を取り組ませたところ,正答率が48.1%であったのに対し,実践後(翌日)の正答率は90.3%と大幅に増加した。
このことから,予習・ノート指導・発表や質問・振り返りをもとにした,児童の思考のつながりに着目した学習は文章問題(数量関係)に成果があったと考えられる。
(2)今後の課題
実践後の翌日の問題の不正答率10%の児童は「自分の答えにはどれくらい自信がありますか。」というアンケートに「自信がある」と肯定的な評価をしていたのにもかかわらず,正答を得ることができなかった。自立解決や全体での学び合いに際し,当該児童らにとって手立てが十分でなかったと考えられる。今後は,これらの児童らを全体の思考のつながりをつくる際の指導の中心におき,さらに関わりを深められるような指導の在り方について検討していきたい。
- 参考文献
-
- 学習指導要領解説(文部科学省 2008)
- 『わくわく算数』指導書第2部詳説 別冊1 指導資料集 3年下
((株)新興出版社啓林館 小学校算数編集部)
|
|||