倍概念を育む指導の工夫

東京都板橋区立板橋第五小学校
福岡　勇人
東京都品川区立延山小学校
宮本　恵美子

1．はじめに〜倍概念の難しさ〜

3年生の担任をしていた頃である。ある児童が文章題を解いているときに，つぶやきが聞こえた。「これは，“倍”って書いてあるから“かけ算”だ。」正しい式は“わり算”である。そのときの，困り果てた児童の表情が忘れられない。“倍”はかけ算なのか，割り算なのか，児童にとって大変難しい問題であることを知った。このことが「倍概念」について研究していこうと考えたきっかけである。

児童の中には，演算決定の際に，問題文の中にかかれている言葉だけで考え，「“分ける”だからわり算」「“倍”だからかけ算」という判断をする傾向がある。たしかに，これまでの学習の経緯を踏まえると，「“倍”だからかけ算」という概念を身につけてきている。2年生では『かけ算』で「倍」の意味を学習しており，「倍」は「幾つ分」を言い換えた言葉として定義されている。しかし，3年生では「倍」を求める方法は『わり算』であるということを学習することになる。この学習のあたりから，「倍」はかけ算なのか，わり算なのか，児童がわからなくなる場合が多い。

また，『特定の課題に関する調査（算数・数学）』（平成18年7月公表）調査結果より，乗法及び除法の計算の意味理解に課題があり，「倍概念」の理解は児童にとって難しいこともわかった。第4学年については「倍表現が含まれる場面で除法の式を選択する（基準量を求める問題）」での通過率が33.1％と低い。また問題に含まれる数値が小数になる第5学年では28.1％，第6学年では24.0％とさらに低い。

整数の乗法・除法は，第2学年から第4学年までで学習している内容であることから，既習の乗法・除法の計算の意味理解の定着が第4学年の段階でも十分ではないことが分かった。この結果から，基準量を求める場面において除法の式をつくる（選ぶ）ことが特に困難であること，また，場面に小数が含まれると，整数の場合に比べ，その理解は困難であることが明らかになった。

これらのことから，本研究では，児童にとって難しい「倍概念」を，どのように身につけていったらよりよいか考え，指導法を提案していくことを主な内容とする。

2．倍概念の指導の改善を図るための実践

以下の3点を指導の工夫とし，実践を行った。

（1）第4学年で「倍概念」を育む指導を取り入れる。

現行の学習指導要領を分析すると，第4学年において，倍概念に関する記述がなされていないことが分かる。第3学年までで，「第2学年において，倍はかけ算と学習したが，何倍かを求めるときはわり算を用いる。」ということを指導するが，その後，「倍」について児童が学習するのは，第5学年の「小数倍」になってからである。そこで，第4学年においても倍概念を育む指導を取り入れ，児童が継続的に，また，スパイラルに倍概念を理解できるようにした。

（※ただし，新指導要領においては，「小数×整数」「小数÷整数」が導入されている。これにより，第4学年にも倍概念を扱う内容が取り入れられると考えられる。）

（2）比の3用法を統合的に扱う。

本校が使用しているT社の教科書には，整数の場合における比の3用法の問題がばらばらに配列されている。例えば，第1用法，第3用法の問題は「倍の計算」として，〔わり算の筆算（1）〕で扱われている。この“ばらばらに配列されていること”が児童にとってつまずきの原因の一つではないかと考え，各用法を統合的に扱うようにした。

（3）クローズドセンテンスで問題を与え，3者間の関係をつかめるようにする。

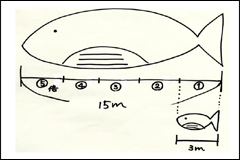
例えば，「親のクジラの体長は15ｍで，子どものクジラの体長は3ｍです。親のクジラの体長は，子どものクジラの体長の何倍ですか。」という第1用法の問題があるとする。この問題を，「何倍ですか。」という問いかけではなく，「5倍です。」という日常文にして児童に提示することで，親クジラ（15ｍ），子クジラ（3ｍ），5倍の3者間の関係をより明確につかませることができると考えた。

この日常文のことを「クローズドセンテンス」とする。今回の実践では，以下のようなクローズドセンテンスを与えた。

3．倍概念の指導の改善を図るための指導の実際

（1）調査方法

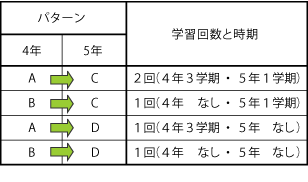
「倍概念」を理解するには，どのような指導時期，指導回数がよりよいのかを考えるため，2つの学級を使って実験的な効果測定を行った。それは以下の通りである。

A，B2つの学級がある。第4学年の3学期に，A組にクローズドセンテンスで問題を与え，整数における比の3用法を統合的に扱う指導を行う。B組では行わない。その後，第5学年に進級する際，均等に学級を分割する。第5学年で分割された学級をC組，D組とし，第5学年の1学期にC組において，同様の指導を行う。すると，たとえば，4年でA組，5年でC組の児童は，2度学習を行ったことになる。4年でB組，5年でC組の児童は，4年のときには学習せず，5年で1度だけ学習することになる。そのように考えていくと，今回調査の対象となる児童は4パターンに分かれる。この4パターンの児童の反応を分析していくことで指導方法，指導時期，指導回数等をどのようにしていったらよいか，検討していく。

（2）実践事例

前記した3つの工夫をもとに授業を計画し2つの小学校（A校B校）で実践を行った。

以下，授業の流れと実際の児童の反応を報告していく。

【第1時】

ねらい：

クローズドセンテンスの課題を模式図に表し，かけ算とわり算の関係をとらえる。
※模式図とは，テープ図や数直線など，問題文におけるそれぞれの関係を図に表したもののことである。

課題を与える。

親クジラの体長は15ｍです。

子どものクジラの体長は3ｍです。

親のクジラの体長は，子どものクジラの体長の5倍です。

この課題の関係を模式図に表す。

線分図や絵で表す児童が多かった。

22名中，20名の児童が図式化できた。図式化できなかった児童は2名で，二量の関係を図の中に表せていなかったり，数値を記入していなかったりした。

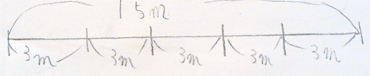
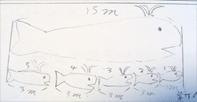
全体で発表・検討を行う。

線分図と絵を取りあげ，それぞれの表し方のよさを話し合い，問題文に出てくる数値がそれぞれ図のどの箇所にあたるかを確認した。

児童の感想（一部抜粋）

クローズドセンテンスで問題を与えたことにより，多くの児童が「親クジラ（15ｍ），子クジラ（3ｍ），5倍」の関係を模式図に表し，3者間の関係を明確にとらえることができていた。また，図にあらわすよさに多くの児童が気付いていることがわかった。かいた図から，演算を決定することができるということにも気付いていたり，かけ算とわり算のつながりを見抜いていたりする児童もいた。

【第2時】

ねらい：

クローズドセンテンスの課題を模式図に表すことでかけ算とわり算の関係をとらえ，整数における比の3用法の問題をとく。

第2時では，3用法すべての問題を与え，問題を図式化させて自力解決させる。

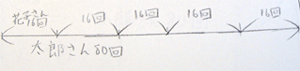
第1用法の問題を与える。

（児童の反応：模式図，式の正誤及びその人数【A校】）

					立式の正誤及び人数
第1用法	図の種類及び人数		図の正誤及び人数		○	×	無答
I ―	テープ図・線分図	13	○	13	13	0	0
			×	0	0	0	0
I ―	数直線	0	○	0	0	0	0
			×	0	0	0	0
I ―	関係図	7	○	3	3	0	0
			×	4	3	0	1
I ―	素朴な図・未完成な図	5	―	―	3	1	1
I ―	無答／式のみ	2	―	―	1	0	1
合計人数（※児童数・・・27）		27			23	1	3

第1用法については，「テープ図・線分図」で表す児童が多く，その図は，正しく関係をとらえていると言える。関係図をかこうとしたとした児童は，太郎さんと花子さんの関係を表す矢印の向きや倍の関係が読み取れず，苦労した様子であった。

図が正しくかけている児童は立式も正しく，また，立式ができていない児童は図もかけていないということがわかった。

※B校では次のような問題を与えた。

（児童の反応：模式図，式の正誤及びその人数【B校】）

					立式の正誤及び人数
第1用法	図の種類及び人数		図の正誤及び人数		○	×	無答
I ―	テープ図・線分図	18	○	11	11	0	0
			×	7	5	1	1
I ―	数直線	0	○	0	0	0	0
			×	0	0	0	0
I ―	関係図	2	○	0	0	0	0
			×	2	2	0	1
I ―	素朴な図・未完成な図	2	―	―	2	0	0
I ―	無答／式のみ		―	―	0	0	0
合計人数（※児童数・・・22）		22			20	1	1

第1用法では，22名中，11名の児童が三者関係を図式化できた。22名中，20名の児童が立式でき，図式化できた児童は，全員正しく立式できた。4名の児童が2種類の線分図を作図していた。

図が誤答の児童は，比例関係ではなく，二量の差に着目してしまったり，三者関係を作図できていなかったり，正しい数値が記入できていなかったり，比例関係をつかめていなかった。「絵」で図式化しようとしているが比例関係を明らかにできていなかったこともあり，矢印等を使って三者関係を明らかにさせる指導や，それぞれの数値が何を表す数値化か明らかにさせる指導の必要性を感じた。「言葉の式」で三者関係を明らかにしている児童もいた。

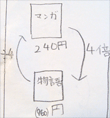
第2用法の問題を与える。

（児童の反応：模式図，式の正誤及びその人数）

					立式の正誤及び人数
第2用法	図の種類及び人数		図の正誤及び人数		○	×	無答
II ―	テープ図・線分図	18	○	17	17	0	0
			×	1	1	0	0
II ―	数直線	0	○	0	0	0	0
			×	0	0	0	0
II ―	関係図	25	○	24	24	0	0
			×	1	0	0	1
II ―	素朴な図・未完成な図	6	―	―	5	0	0
II ―	無答／式のみ	1	―	―	1	0	0
合計人数（※児童数・・・50）		50			48	1	1

第2用法では，「関係図」で表す児童が多く，そのほとんどは正しく図がかけているといえる。マンガの値段（240円）と物語の値段（□円）の関係を表す矢印や，その関係が4倍であることが図に表されており， 立式へとスムーズにつながっている。

「テープ図・線分図」で表す児童は第1用法に比べると少なくなっている。第2用法でも，図が正しくかけていると立式も正しいことがわかった。

図式化できなかった児童は数値が正しく記入できていなかった。また，立式が無答の児童は数値関係を明らかにすることができていない。立式できた児童は「絵」で三者関係を明らかにしていた。

第3用法の問題を与える。

（児童の反応：模式図，式の正誤及びその人数）

					立式の正誤及び人数
第3用法	図の種類及び人数		図の正誤及び人数		○	×	無答
III ―	テープ図・線分図	20	○	17	17	0	0
			×	3	2	0	0
III ―	数直線	0	○	0	0	0	0
			×	0	0	0	0
III ―	関係図	18	○	16	16	0	0
			×	2	2	0	0
III ―	素朴な図・未完成な図	6	―	―	5	0	1
III ―	無答／式のみ	5	―	―	3	0	1
合計人数（※児童数・・・49）		49			45	1	3

第3用法では，「関係図」で表す児童が多いが，第2用法ほどではない。第1用法，第2用法と同様に，図が正しくかけている児童は，立式も正しいことがわかった。

立式できなかった児童は二量の関係をつかめていなかった。図式化できなかった児童は，数値を正しく記入できていなかったり，二量の関係を明らかにしていなかったり，二量の差に着目してしまっていた。

児童の感想

第1時で模式図に表すことのよさに気付いている児童は，クローズドセンテンスではなく，通常の問題においても進んで模式図に表すことができた。そうすることで「基準量」「比較量」「割合」の3者関係を明確につかむことができていた。

実践事例2については，A校のみの実践となる。

【第1時】

クローズドセンテンスの課題を模式図に表し，小数場面におけるかけ算とわり算の関係をとらえる。

課題を与える。

7.2リットルのスープがあります。

3つのなべに同じ量ずつ分けます。

ひとつ分は2.4リットルになります。

　

この課題の関係を模式図に表す。

線分図や絵で表す児童が多かった。与えられたセンテンスを「7.2÷3＝2.4」という形の式に表している児童もいた。

全体で発表・検討を行う。

線分図と絵を取りあげ，それぞれの表し方のよさを話し合った。与えられたセンテンスと，児童がかいた絵，式がつながっていることを確認した。

また，提示したクローズドセンテンスを用いて以下のような指導を行った。

7.2リットルのスープがあります。

3つのなべに同じ量ずつ分けます。

ひとつ分は2.4リットルになります。

適応題に取り組む。

以下のようなオープンセンテンス（通常の問題文）を3題与えた。

【ア】

ある量のスープがあります。このスープを3つのなべに同じように分けると、ひとつ分は2.4リットルになりました。スープは全部で何リットルありましたか。

【イ】

7.2リットルのスープがあります。このスープをいくつかのなべに同じ量ずつ分けると、ひとつ分は2.4リットルになりました。いくつのなべにわけましたか。

【ウ】

7.2リットルのスープがあります。
このスープを３つのなべに同じ量ずつに分けると、ひとつ分は何リットルになりますか。

絵や線分図，数直線で表す児童が多かった。それぞれの立式の正答率を示す。

（各問題における立式正答者数）

問題【ア】	問題【イ】	問題【ウ】
27／30	28／30	26／30

オープンセンテンスの問題が，クローズドセンテンスをもとに作られているということを考慮しなくてはいけないが，高い立式正答率といえる。

児童の感想

第4学年における「実践I」と同様に，クローズドセンテンスを与えたことにより，模式図に表すことができた。3者の関係（7.2リットルのスープ　3つのなべ　ひとつ分は2.4リットル）をとらえることができていた。

4．実態調査〜授業を終えて〜

すでに前述しているが，今回の実践は，以下の4パターンの児童を対象としている。

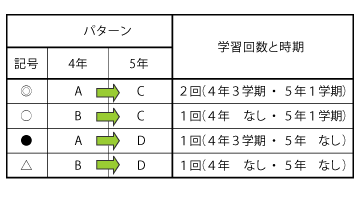
それぞれの児童に対して実態調査を行った。調査問題は以下の通りである。

1	さやかさんがとんだなわとびの回数は52回です。これはひろしさんのとんだ回数の4倍です。ひろしさんは，何回なわとびをとびましたか。	第3用法 （整数）
2	牛乳が0.8リットルあります。オレンジジュースは牛乳の4倍の量があります。オレンジジュースは何リットルありますか。	第2用法 （小数）
3	ゆりさんは犬とねこをかっています。犬の体重は4.8ｋｇ，ねこの体重は1.2ｋｇです。犬の体重は，ねこの体重の何倍になりますか。	第1用法 （小数）
4	A小学校の面積は12.8km2です。これは，B小学校の面積の0.6倍です。Ｂ小学校の面積は何km2ですか。	第3用法 （小数）

結果は次の通りである。

（調査日：平成20年11月21日）

パターン	正答率 （問1）	正答率 （問2）	正答率 （問3）	正答率 （問4）	4問正答者数	計
◎	14/15 93%	12/15 80%	14/15 93%	9/15 60%	6人	49/60 81%
○	9/12 75%	9/12 75%	11/12 91%	10/12 83%	6人	39/48 81%
●	13/15 86%	13/15 86%	15/15 100%	11/15 73%	7人	52/60 86%
△	11/14 78%	8/14 57%	14/14 100%	13/14 93%	4人	49/56 82%
計	83%	75%	96%	76%

※例えば「14／15」の場合は，その問題において15名のうち，14名が正答したことをあらわす。

※「4問正答者」は全問正答することができた児童の数である。

さて，結果を見ると，難しいとされている「小数における倍概念」が正しく身に付いている児童が多い。特に問4は基準量を求める第2用法の問題であり，さらに数値が小数になっている。『特定の課題に関する調査（算数・数学）』（平成18年7月公表）調査結果と比較しても，今回の調査はそれを大きく上回る結果となった。このことは，児童が「倍」という言葉に惑わされずに，自ら模式図などをかき，関係を正しくつかむことができたということであり，本実践が一定の成果をあげることができたと考える。ただし，4つのパターン（◎・○・●・△）の児童の反応に大きな差を見ることはできなかった。このことは，実践や調査が年度をまたぐなど，時間的な間隔が大きく空いてしまったこと，実践数が足りなかったこと　などが挙げられる。これらのことを今後の課題としていく。

5．終わりに〜成果と課題〜

（1）成果

児童にとって難しいとされる「倍概念」を育む指導について，指導時期，指導回数，指導方法を検討し，実践をすることができた。特に指導方法については，クローズドセンテンスで問題を与えること　比の3用法を統合的に扱うことが有効であることがわかり，一定の成果を得ることができた。

（2）課題

指導時期や指導回数については，まだまだ検討の余地がある。指導方法についても，成果である2点を柱にしながら，よりよい方法はないか検討していきたい。

	審査委員会の講評 倍概念を育む指導の工夫 倍概念は児童にとって理解が難しい学習内容の一つである。過去調査の結果や児童の実態，教材に関する考察を基に，なぜ難しいのかを明確にし，指導改善の工夫を３点に焦点化して研究を進めている点で高く評価できる。また，線分図や数直線などの図の使用，及び立式を視点とした児童の反応の分析内容も興味深い。研究の進め方，実践内容の分析，ともに明瞭かつ示唆的であり，実践研究を基盤とした更なる指導案の提案が期待できる。