
授業実践記録(数学)
平面図形における義務教育9年間の学びをつなぐ教材開発の研究
-正多角形による「敷き詰め」活動を取り入れた授業づくりからの考察-

Ⅰ はじめに
本研究は,佐賀大学文化教育学部附属の小学校算数科と中学校数学科が共同で研究している共通の教材開発を目的とする。具体的には,正多角形による「敷き詰め」活動を取り入れた授業を通して,義務教育9年間の算数・数学の学びをつなぐ教材として有効であるかを検証していく一部を紹介する。そして,本研究を通して,「敷き詰め」にある幾何学的な操作から,図形の性質の根底にある本質的なものを見抜く直観力に繋がる教材として,算数・数学の授業に積極的に取り入れることができることを期待したい。
Ⅱ 研究の実際
1 単元の実際
(1) 単元名 1年 平面図形
(2) 単元を貫く問い
図形の関係性や対称性は?
(3) 内容
小学校算数科での図形の学習は,操作的な活動や直観的な取り扱いを中心として,図形についての感覚を育てる。同時に,図形の概念や簡単な図形の性質を活用して,判断したり,表現したり,処理したりできるようにすることをねらいとしている。これに続く中学校第1学年の平面図形の学習では,対称性に着目させ,見通しをもって図をかくこと,観察,操作や実験を通して,図形に対する直観的な見方や考え方を養うとともに,論理的に考察し表現する能力を培う。また,本単元の授業を進める際,図形の対称性についての1つの図形の性質から,2つ以上の図形の間の関係を捉えさせる。また,直線の位置関係や対応する辺や角の相等関係など,図形に関する理解が深まるよう指導することを大切にしていく。
2 授業の実際
(1) 「敷き詰め」に対する生徒の実態
本校第1学年の1クラス(本時実施クラス)を対象に,小学校の算数の学習から「敷き詰め」のイメージがあるか意識調査を行った。
調査時期: 2013年5月6日
調査方法: 連想法*1
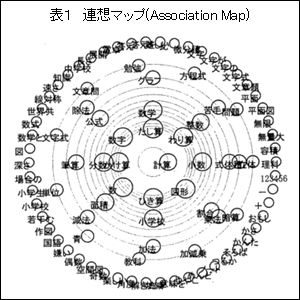
調査では,提示語を「算数」とし,生徒に「算数」に対する浮かんだイメージを言葉としてできるだけ多く書かせた。その結果をまとめたものを次に示す(表1)。
*1 上薗恒太郎(長崎大学教育学部名誉教授)
このマップでは,円の中心に近づくほど,多くの回答があったことになっているが,「敷き詰め」のカテゴリーは見つからない。また,この調査では,生徒が記入したカテゴリーすべてがわかるのだが,「敷き詰め」に関しては一つもなかった。つまり,算数の既習内容として,「敷き詰め」の学習がなされていなかったか,行われていたにしても意識の低い学びになっていることが,この調査を通していえる。
そこで,生徒は「敷き詰め」活動に不慣れであると判断し,単元構成の3時間計画で「敷き詰め」活動を取り入れた授業を行うことにした(表2)。
| 1時間 | 任意の四角形による敷き詰め |
|---|---|
| 1時間 | 正多角形による敷き詰め |
| 1時間 | 敷き詰めの作品づくり |
(2) 平面上における任意の四角形による「敷き詰め」活動を取り入れた授業実践
まず初めに,既習内容である「四角形の内角の和が360°であるのはどうしてか?」とたずねた。すると,生徒たちから即座に「三角形が2つあるから」という答えが返ってきた。そこで,一人の生徒にその図を板書させ,全員で確認をした。その際,教師の方で,描いてもらった図を使い,「この状態が四角形の中に2つの三角形が敷き詰められているということだよ。」と図形の敷き詰めに関しても確認をさせた。
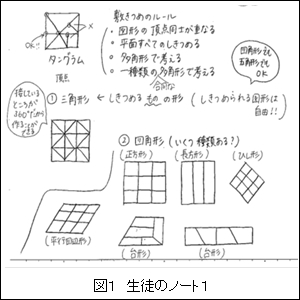
次に,図形の敷き詰めに関わってのルールを確認させた。図形を敷き詰める活動の中では,条件次第でねらいが違ってくる。今回の学習において,全員で敷き詰めのルールを確認させた。その時に,1点に各頂点が集まる条件を理解させるために,生徒たちが知っていたタングラムを活用した。
そして,授業の目標である任意の多角形を敷き詰める活動に入っていった。生徒たちは,まず最も小さな多角形である三角形の敷き詰めを考えようとした。その後,四角形,五角形などの敷き詰めにすすんでいく生徒が出てきた。時間を確保し,自由に考えさせた。また,いろいろな四角形があることから,生徒に「四角形の敷き詰めには何種類あるの?」と加えて問いを提示した。この活動をしている時,何人かの生徒から「1点に集まる角の和が必ず360°になる」というつぶやきが聞こえてきた。授業の様子がわかる生徒のノートを紹介する(図1)。
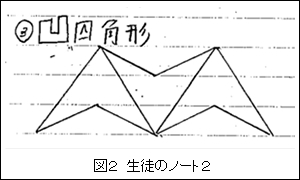
最後に,紹介したい四角形の敷き詰めは,中学第2学年でよく見かける学習内容に繋がるものである(図2)。
(3) 正多角形による「敷き詰め」活動を取り入れた授業実践
前時の振り返りを行う中で,敷き詰めのルールを確認してから,本時の課題を提示した(写真1)。
課題1として,1種類の正多角形を使って,平面を敷き詰めることを考えさせた。この課題に対して,ほとんどの生徒が正三角形から正方形,正五角形…と大きさの順に考え,ワークシートにまとめていた(図3)。
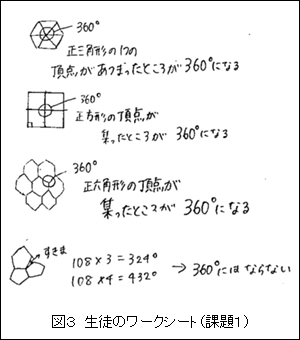
図3のまとめからもわかるように,多くの生徒が,1点に集まる角の大きさの和に着目して,敷き詰められる正多角形を探していた。ここで,前時の学習で気づいた敷き詰めの条件として,1点に集まる角の和が360°であることが有効に利用できた。その成果として,課題1の活動では,大半の生徒が正三角形,正方形,正六角形の3種類の敷き詰めを考えていた。この後,実際に黒板の方で,希望する生徒に敷き詰めを行わせた。(写真2)。

写真1 敷き詰めのルール確認と課題の提示

写真2 課題1の敷き詰めを行っている場面
次に,「1種類の正多角形の敷き詰めで,本当に3種類しかないといえるか。」という問いを投げかけた。ほとんどの生徒が,3種類しかないと言っていたが,その根拠についてはうまく説明できない生徒もいた。
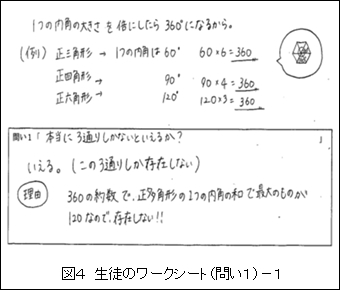
では,生徒の考えをいくつか紹介する。1つ目として,敷き詰めの条件となる1点に集まる角の和が360°の図形的な結果から,説明をしたものである(図4)。
この生徒は,ワークシートには記述していないが,おそらく360の約数でその数を除いた時の最大の数は180であることを知っている。しかし,正多角形で考えているので最大が120という約数になることが,正多角形の1つの内角の和で最大のものの文章から気づいているものと思われる。
次に紹介する生徒は,3種類しかないという根拠をしっかりと説明ができている(図5)。
 |
 |
課題1の取り組みを通して,生徒の思考の中で,mx=360°(mは1点に集まる面の数,xはその場面の正n角形の1つの内角の大きさ)の関係に気づいていることがわかった。また,3種類しかない根拠については,中学3年の因数分解を学習後,![]() の関係から,導かせることが可能となる。
の関係から,導かせることが可能となる。
課題2では,正多角形の組み合わせで敷き詰めが可能かどうかを考えさせた。ここでは,実際に正多角形を各グループに与え,まわりと試行錯誤しながら2種類の正多角形で敷き詰めることに取り組ませた。実際の図形があるため,グループで協力しながら楽しんで活動していた。そして,2種類の正多角形を使って敷き詰められた時は,グループみんなで喜ぶ姿が見られた。また,活動の中で,ただ単に教具を使うだけでなく,敷き詰められる条件として1点に集まる角の和が360°であることを考えながら,正多角形の組み合わせに取り組んでいた。実際に,授業の中で発見された敷き詰めを紹介する(写真3,4,5,6,7)。
※表示(3,6,3,6)は,正三角形と正六角形が1点のまわりにこの順序に並ぶことを表す。
黒板では,紹介できなかったが,グループの中で敷き詰められていたものを紹介する(写真8)。
十分な時間を確保できない中,予想以上に組み合わせによる敷き詰めを完成させたグループが多かった。そして,グループの中には,3種類以上の正多角形を使って敷き詰めに挑む様子も見られた。ただ,順調に敷き詰めることができなかったグループもあった。その正多角形の組み合わせを紹介する(写真9)。
この組み合わせは,1点に集まる角の和が360°になる箇所がある。
 写真3(3,6,3,6) |
 写真4(3,3,3,3,6) |
 写真5(3,3,3,4,4) |
 写真6(3,3,4,3,4) |
 写真7(4,8,8) |
 写真8(3,12,12) |
 写真9(5,5,10) |
正五角形の1つの内角の大きさ 108°×2=216°
正十角形の1つの内角の大きさ 144°
合わせると,360°となる。
この結果から,生徒たちは混乱したのである。これまで敷き詰め可能となる条件であったもので,敷き詰めることができなくなったのである。
この場面については,授業の中で実際に黒板で操作をさせ,敷き詰めることができないことを確認させた。つまり,この結果から,1点に集まる角の和が360°であることは,敷き詰め可能としての十分条件になり得なかったということがいえたのである。この確認をした所で,本時の授業は終了した。
Ⅲ おわりに
現行の啓林館の教科書では,小学5年下に正多角形の内容があり,児童は学びを始める。中学1年では,既習内容を活用して今回のような学びを行い,図形の性質の根底にある本質的なものを見抜くことに繋げていくことができた。さらに,本教材は,中学3年や高校数学の学びの中でも扱うことができる。今回の課題2における学びは,発展性のあるものであろう。


