
|
式の意味を正しくとらえる児童の育成 | ||
|
|||
|
1.はじめに 1年生の児童は,動物や食べ物の具体物や数図ブロックを操作しながらとても楽しそうに学習に取り組む。数の合成・分解では,具体物を操作しながらなら,「7個は2個と5個」と多くの児童が答えられる。ところが,「7は2と□」と数字だけで表わされると,何を答えればよいのか分らなくなったり,7と2をたしてしまったりして戸惑う姿が見られる。これは,問題場面に含まれる数の関係を,具体物と対応させて正しくつかむことができていないことに原因があると考える。そこで,加法や減法の学習において,式が何を表しているのかに気付いたり,立式の誤りに気付いたりできるようになるために,問題場面と式を関連付けて考えるようにさせることが大切である。 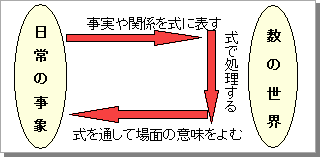 こうすることによって,右図のように「事実や関係を式に表す」「式で処理して考えを進める」「式を通して場面の意味をよむ」などの力を併せもち,日常の事象と数の世界を結び付ける,「式の意味を正しくとらえる児童」を育成できると考えた。 こうすることによって,右図のように「事実や関係を式に表す」「式で処理して考えを進める」「式を通して場面の意味をよむ」などの力を併せもち,日常の事象と数の世界を結び付ける,「式の意味を正しくとらえる児童」を育成できると考えた。2.単元名「あわせて いくつ ふえると いくつ」 3.単元の目標
4.指導計画(8時間完了)
5.授業の実際(第4時)
6.授業を終えて これまでの指導では,増加では右側から増える場面を取り上げるだけで終わっていた。本時は,いろいろな方向から増える場面を取り上げたことにより,加数と被加数の関係について話し合いによって明確にすることができた。これらのことから,1年生での加法や減法の意味をとらえさせる指導では,1場面での数図ブロックの操作の仕方に合わせて立式させるだけでなく,いろいろな場面を取り上げて考えさせることが,正しく式に表す上で有効であることが分かった。 7.おわりに 本実践では,和が10以下の加法について述べてきたが,和が10より大きい数になる加法及びその逆の減法,3つの数の計算,乗法・除法においても,「式の意味を正しくとらえる児童」を育成することが大切である。特に,「式に表す」「式で処理する」と同様に「式をよむ」活動を重視する必要があると感じる。今後は,問題場面と解決方法と式を関連付けられるような工夫を,実践を通して探っていきたい。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|
 くるまが5だいあります。
くるまが5だいあります。


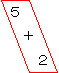 になるのかな。
になるのかな。