| 学習活動 |
教師の指導と支援と児童の反応 |
| 教 師 |
児 童 |
| 1.課題を知る。 |
シの陣地の面積は,どれだけになるか考えよう。
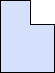 |
|
| 2.解決の方法を考える。 |
・複合図形をどうすれば正方形や長方形と同じように,面積を求めることができるでしょうか。
・切り離したり,図形に線を引いたりすれば求められそうだね。 |
・分ければ面積がわかります。
・線を引いてもいいですか。
・切ってもいいですか。 |
| 3.複合図形の面積を調べる。 |
 |  |
| 【個人解決の様子】 | 【発表の準備】 |
|
・図に言葉や記号等を記入させ,筋道を立てた説明ができるようにさせる。
・全体から部分を引く方法のヒントカードを用意し,その方法で解決させる。 |
|
| 4.全体で話し合う。 |
(児童による3つの方法の発表の後)
・この方法に名前をつけましょう。1の方法は何とつけましょうか。
・いい名前ですね。
・このやり方で他のも名前をつけましょう。 |
・たてに線を引いたので「たてくぎり」がいいと思います。
・2の方法はよこに線を引いたので「よこくぎり」です。
・3の方法はたして区切るので「たしくぎり」です。 |
 |
 |
 |
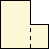
方法1
「たてくぎり」 |
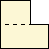
方法2
「よこくぎり」 |
方法3
「たしくぎり」 |
|
|
・こんな図形では,どの方法がいいのかな。
|
・形によって3つの方法を使い分けていくと簡単にはやく面積を求められそうですね。
・サの面積を求めてシと比べてみましょう。 |
・アは,「たしくぎり」が簡単です。
・イの形は,「よこくぎり」や「たてくぎり」でもできるけど,「たしくぎり」が簡単です。
・ウの形は,ぜったい「たしくぎり」が簡単です。 |
| 5.練習する。 |
・実は,もう1つ方法がありました。このやり方がわかったら先生に教えてください。 |
| ・授業終了後に数名の児童が早速黒板のところに集まり,やり方を考えていた。 |
|
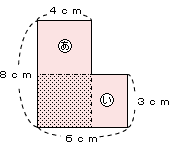 |
 8×4=32 8×4=32
 6×3=18 6×3=18
? 3×4=12
(32+18)-12=38
こたえ 38cm2
|
|

【教師が提示した方法を考えている児童達】
|







