答
答は1通りとは限らない.
ここにはすべての答が書いてあります.
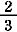 |
=  + + 
|
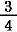 |
=  + + 
|
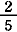 |
= 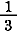 + + 
|
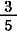 |
=  + + 
|
 |
=  + +  + +  = =  + + 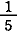 + + 
|
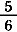 |
=  + + 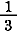
|
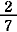 |
=  + + 
|
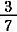 |
= 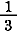 + +  + +  = = 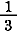 + +  + +  = = 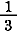 + +  + + 
|
|
= 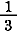 + +  + +  = =  + +  + +  = =  + + 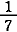 + + 
|
 |
=  + + 
|
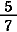 |
=  + + 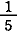 + +  = =  + +  + +  = =  + + 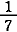 + + 
|
 |
=  + + 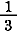 + + 
|
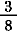 |
= 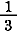 + +  = =  + + 
|
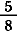 |
=  + + 
|
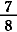 |
=  + + 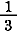 + +  = =  + +  + + 
|
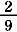 |
= 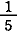 + +  = =  + + 
|
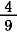 |
= 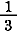 + + 
|
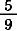 |
=  + + 
|
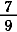 |
=  + +  + +  = =  + +  + + 
|
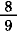 |
=  + + 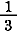 + + 
|
参考文献
[1] チェイス著 平田寛監修 吉成薫訳 リンド数学パピルス 朝倉書房 1985
[2] マリオ・リヴィオ著 斉藤隆央訳 黄金比はすべてを美しくするか? 早川書房 2005
話題1 初代ローマ皇帝の遺言状
●初代ローマ皇帝の遺言状●
ローマ人もまたこのような記数法を用いた.
初代ローマ皇帝アウグストゥスの遺言状は次の一句から始まる.
|
「無慈悲な運命がわたしからガイウスとルキウスの息子二人までも奪い去ってしまった.
|
|
ティベリウスに遺産の二分の一と六分の一を譲ることをここに言明する」
|
|
(塩野七生 ローマ人の物語 新潮社文庫本第17巻24ページ)
|
「二分の一と六分の一」は  + +  = = 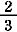 である. である.
彼らにとっては, 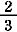 は2÷3でもなければ「三分の一が2つ」でもなく「二分の一と六分の一」でなければならなかった.繰り返すが,分母と分子から構成される分数という概念はなかった.また,小数の概念もなかった. は2÷3でもなければ「三分の一が2つ」でもなく「二分の一と六分の一」でなければならなかった.繰り返すが,分母と分子から構成される分数という概念はなかった.また,小数の概念もなかった.
ちなみに,アルキメデスの著作集を調べてみたが  , , 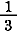 , ,  の記述はあるが の記述はあるが 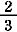 , , 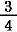 などはなかった. などはなかった.
このことから,古代エジプト人の分数の表現は,エジプト,ギリシャ,ローマ時代を通して使われていたと推定できる.
話題2 単位分数分解
●単位分数分解●
分数 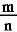 を,異なる自然数の逆数の和 を,異なる自然数の逆数の和
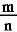 = =  + +  + +  +… ( +… (  < <  < <  <…) <…)
と表すことを 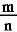 の単位分数分解と呼ぶことにしよう. の単位分数分解と呼ぶことにしよう.
●標準分解●
そもそもどんな分数も異なる単位分数の和になるだろうか.
これは意外に簡単に解決する.
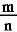 が単位分数でない場合 が単位分数でない場合
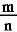 より小さい最大の単位分数 より小さい最大の単位分数
を考えればよいのである.
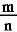 を単位分数で近似するという意味でこれが最良の近似数である. を単位分数で近似するという意味でこれが最良の近似数である.
m 個の連続整数 n,n+1,n+2,…,n+m−1 のうちには必ず m の倍数がある.これを mn1=n+k とすると,等式
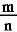 = =  + +  (0≦k<m) (0≦k<m)
が成り立つ.
この等式を
(与えられた分数)=(最良近似の単位分数)+(誤差項)
と見る.
ここで注目すべきは誤差項を表す分数  の分子がもとの分数 の分子がもとの分数 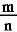 の分子よりも小さいことである. の分子よりも小さいことである.
そこで次の手続きを考える.
) (1) (1) |
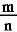 が単位分数でない場合, が単位分数でない場合, 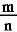 よりも小さい最大の単位分数を よりも小さい最大の単位分数を  とする とする
|
) (2) (2) |
 が単位分数でない場合, が単位分数でない場合,  よりも小さい最大の単位分数を よりも小さい最大の単位分数を  とする とする
|
) (3) (3) |
 が単位分数でない場合, が単位分数でない場合,  よりも小さい最大の単位分数を よりも小さい最大の単位分数を  とする とする
|
| (4) |
…
|
この操作を続けると,誤差項を表す分数の分子はだんだん小さくなるからついには0となり,
となる.
以上により,どんな分数も異なる自然数の和として表せることが分かった.
このようにきまる単位分数分解

を標準単位分数分解と呼ぼう.
例  の標準分解 の標準分解
| 第1項 |
|
 の分母を14の倍数(最小にとる)で置き換えると の分母を14の倍数(最小にとる)で置き換えると  = =  (これが第1項) (これが第1項)
第1項の残りは  − −  = = 
|
| 第2項 |
|
 の分母を11の倍数で置き換えると の分母を11の倍数で置き換えると  = =  (これが第2項) (これが第2項)
第2項以下の残りは  − −  = =  = = 
|
| 第3項 |
|
 の分母を5の倍数で置き換えると の分母を5の倍数で置き換えると  = =  (これが第3項) (これが第3項)
第3項以下の残りは  − −  = =  = =  (逆数なのでこれが最終項) (逆数なのでこれが最終項)
|
よって, の標準分解は の標準分解は
 = =  + +  + +  + + 
となる.
●単位分数分解は一意ではない●
例えば,
●いくらでも長い単位分数分解が存在する●
 だから,最後の項 だから,最後の項  を を  に置き換えることにより,いくらでも長い単位分数分解をつくることができる. に置き換えることにより,いくらでも長い単位分数分解をつくることができる.
●初項はいくらでも小さくとることができる●
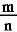 > >  となる単位分数 となる単位分数  を任意にとったとしよう. を任意にとったとしよう.

であるから,ある p に対し不等式


が成り立つ.
そこで, の標準分解を の標準分解を

とすると,単位分数分解

が得られる.
ここで,

であるから,
n1 < n1+1 < n1+2 < … < p < q1 < q2 < … < qr
が成り立つ.
話題3 埋もれてしまった数学
●埋もれてしまった数学●
以上の結果は単位分数分解について数学の理論としては否定的な資料となるものである.つまり,単位分数分解を考えても大した理論にはならないということである.
現代の数学ではエジプト人の分数は顧みられることはない.
歴史的には埋もれてしまっている.こんにちでは役に立たない数学である.
しかし,これも文化遺産である.
我々の文化は過去の文化の繁栄と衰退の上に立っている.
話題4 パズルとしての単位分数分解
●パズルとしての単位分数分解●
分数の単位分数分解は数学の理論にはならないがパズルとしては生き残る可能性がある.
分数を
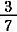 = =  + +  + + 
のように表せというパズルについて考えてみよう.
パズルとして出題するからには,あらかじめ解の存在は保証しなければならない.
(1) 解は一意とは限らない.
|
|
すでに見たように,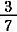 , ,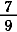 は複数解をもつ: は複数解をもつ:
したがって,「すべての解を求めよ」が課題となるであろう.
せめて2項の分解 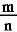 = =  + +  は一意解かと思ったが,これにも反例がある. は一意解かと思ったが,これにも反例がある.
|
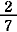 = = 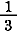 + +  = =  + + 
|
|
 = =  + +  = = 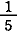 + +  = =  + +  (3つもある) (3つもある)
|
すべての解を見つけるとなると結構落とし穴が待ちかまえている.あなどるわけにはいかない.
|
(2) 最短表現
|
|
例えば 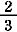 は次の分解をもつ. は次の分解をもつ.
|
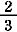 = =  + + 
|
|
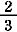 = = 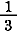 + +  + + 
|
|
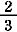 = = 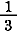 + + 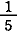 + +  + + 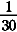
|
|
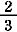 = =  + + 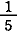 + +  +… (理論的に可能) +… (理論的に可能)
|
このほかにも無数の分解が存在するが,パズルとして使えるのは 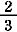 = =  + +  だけである. だけである.
パズルとしては,項数の少ないもの「最短表現」が対象となろう.
|
(3) 標準分解が最短とは限らない.
|
|
例えば,  の標準分解は の標準分解は
 = = 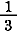 + +  + + 
であるが,この分数には
 = =  + + 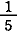
という短い分解がある.
標準分解は,「どんな分数も逆数の和として表される」という例を示すだけのものである.ただ,この分解は数学的にはごく自然なものであるから標準と冠したのである.標準分解はパズルとは直接的には結びつかない.しかし,次に述べるように標準分解は答を見つけるヒントにはなる.
|
(4) 試行錯誤
|
|
逆数分解のパズルは試行錯誤で探すしかない.
しかし,試行錯誤といってもまったく方針がないわけではない.
しらみつぶしに調べるためには標準分解が1つのヒントになる.
「第1項を最大にとる」のが標準分解である.そこで「標準分解のある項を小さくとる」ことで他の解を見つける手がかりとする.
例えば 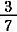 の場合 の場合
標準分解は 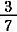 = = 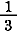 + +  + +  である である
この第1項を  とすることにより,もう1つの解 とすることにより,もう1つの解 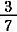 = =  + + 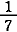 + +  が見つかる. が見つかる.
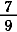 の場合 の場合
標準分解は 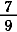 = =  + +  + + 
この第2項を小さく(  → →  )することにより )することにより 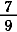 = =  + +  + +  が見つかる. が見つかる.
 の場合 の場合
標準分解は  = = 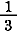 + +  + + 
この第1項を小さくすることにより,最短表現  = =  + + 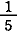 が見つかる. が見つかる.
|
|